Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của SA và AB. Khẳng định nào sau đây đúng ?
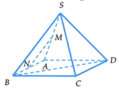
A. M N / / S A B
B. M N / / B D
C. M N / / S B C
D. MN cắt BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
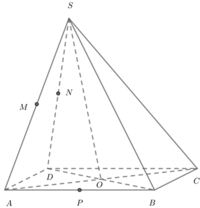
Phương pháp: Xét tính đúng sai của từng mệnh đề.
Cách giải: Ta có 4 điểm M, N, O, P đồng phẳng.


Trong mặt phẳng (ABCD) ta có AC cắt BD tại O, IJ cắt BD tại E. trong mặt phẳng (SBD), ME cắt SO tại G. Ta có G thuộc (MIJ). (MIJ) chứa IJ // AC nên giao tuyến của (MIJ) với (SAC) là đường thẳng qua G và song song với AC.
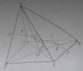
Đáp án D

mình làm cũng hoang mang lắm bạn=), hay để hỏi cô xem sao

+ Ta có IJ là đường trung bình của tam giác SAB nên IJ// AB// CD
=> IJCD là hình thang. Do đó A đúng.
+ Ta có I B ⊂ S A B I B ⊂ I B C ⇒ S A B ∩ I B C = I B . Do đó B đúng.
+ Ta có J D ⊂ S B D J D ⊂ J B D ⇒ S B D ∩ J B D = J D . Do đó C đúng.
+ Trong mặt phẳng (IJCD), gọi IC và JD cắt nhau tại M .,
=> giao tuyến của mặt phẳng (IAC) và (JBD) là MO
Do đó D sai.
Chọn D.
Chọn đáp án C
Do M, N lần lượt là trung điểm của SA và AB nên MN là đường trung bình của ∆ S A B và M N / / S B
Ta có