Cho hình thang cân ABCD có đáy nhỏ AB và hai cạnh bên đều có độ dài bằng 1. Tìm diện tích lớn nhất S m a x của hình thang
A. S m a x = 8 2 9
B. S m a x = 4 2 9
C. S m a x = 3 3 2
D. S m a x = 3 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
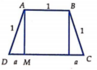
Kẻ AM vuông góc với CD tại M.
Đặt D M = a . Ta có A M = 1 − a 2 ; C D = 2 a + 1
Diện tích của hình thang là
S = 1 2 A B + C D . A M = 1 2 2 a + 2 1 − a 2 = a + 1 1 − a 2
Bài toán trở thành tìm giá trị lớn nhất của hàm số f a = a + 1 1 − a 2 trên (0;1)
Sử dụng chức năng TABLE của máy tính ta nhập

Nhìn vào bảng giá trị ta thấy giá trị lớn nhất của hàm số ≈ 1,299 . So sánh với các phương án chỉ thấy D thỏa mãn, ta chọn D.

1) a) Do ABCD là hình thang cân => góc D = góc C ; góc B = góc A
Trong t/g ABC có : góc A = 90 độ => góc D + góc C2 = 90 độ
Trong t/g ABC có AB = BC ( gt ) => t/g ABC cân tại B => góc A1 = góc C1
Ta có góc A = 90 độ + góc A1 = góc D + góc C2 + góc C1 = góc C + góc C = 2C
Mà :
A + B + C + D = 360 độ = 2A + 2C = 4C + 2C = 6C => góc C = 360 độ : 6 = 60 độ
=> góc C = góc D ( = 60 độ ) ; góc A = góc B ( = 120 độ )

Bạn tự vẽ hình nha ( hình nó dễ )
Gọi F là trung điểm của BC. Cắt hình thang theo đường DF đưa ghép vềnhư hình vẽ, điểm C trùng với điểm B , điểm D trùng với điểm E
Vì AB // CD \(\Rightarrow\)\(\widehat{ABC}+180\)độ \(\Leftrightarrow\)A ; B ; E thẳng hàng
\(\widehat{ABF}+\widehat{DFC}=180\)độ
\(\Rightarrow\)D ; F ; E thẳng hàng
\(\Delta DFC=\Delta EFB\left(g-c-g\right)\)
Diện tích DFC = diện tích EFB
\(\Rightarrow\)Diện tích ABCD = diện tích ADE
\(\Delta DFC=\Delta EFB\left(cmt\right)\)
DC = BE
AE = AB + BE = AB + CD
Diện tích ADE = \(\frac{1}{2}DH.AE=\frac{1}{2}DH.\left(AB+CD\right)\)
Vậy diện tích ABCD = \(\frac{1}{2}DH.AE=\frac{1}{2}DH.\left(AB+CD\right)\)

Kéo dài AB về phía B một đoạn BE=DC. Nối DE cắt BC tại M.
Do CD // BE nên ta có tam giác MDC = tam giác MEB (trường hợp g.c.g). Suy ra dt(ABCD)=dt(ABMD) + dt(MDC) = dt(ABMD) + dt(MEB) = dt(DAE) = 1/2 .AE . h =1/2 (AB + BE).h = \(\dfrac{AB+CD}{2}.h\)
b) Theo câu a) thì diện tích hình thang ABCD bằng diện tích tam giác DAE nên ta nối D với trung điểm N của AE thì DN sẽ chia tam giác DAE thành 2 phần bằng nhau. Khi đó diện tích tam giác DAN bằng nửa diện tích hình thang ABCD.
Đáp án D
Dựng A H ⊥ C D . Đặt D H = x 0 < x < 1
Ta có: D C = 2 x + 1 ⇒ A H = 1 − x 2
S A B C D = 1 + 2 x + 1 2 1 − x 2 = 1 + x 1 − x 2 = f x ⇒ f ' x = 1 − x 2 − 1 + x x 1 − x 2 = 0 ⇔ 1 − x 2 = 1 + x x ⇔ 2 x 2 + x − 1 = 0 ⇔ x = − 1 l o a i x = 1 2 ⇒ S m a x = f 1 2 = 3 3 4 ⇔ x = 1 2