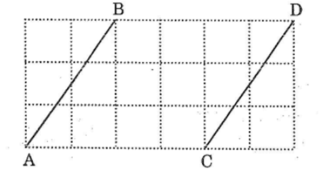
Cho các đoạn thẳng AB và CD trên giấy kẻ ô vuông (hình dưới ). Chứng minh rằng AB = CD, AB // CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
Lê Huy Tường
VIP
8 tháng 3 2021
Xét ∆AHB và ∆ CKD có:HB = KD (= 1 ô)AHBˆ = CKDˆAH = CK (= 3 ô)=> ∆AHB = ∆CKD(c.g.c)=> AB = CD (cạnh tương ứng)Chứng minh tương tự ta đươc: ∆ CEB = ∆ AFD (c.g.c)suy ra BC=AD.b) Xét ∆ABD và ∆CDB có:AB = CD (cmt)BC = AD (cmt)BD chung.=> ∆ABD = ∆CDB (c.c .c)=> ABDˆ = CDBˆMà hai góc này ở vị trí so le trongVậy AB // CD (đpcm)
chả bt có khớp ko chứ lười đọc quá
3 tháng 3 2022
Xét ∆AHB và ∆ CKD có:
HB=KD.
ˆAHB=ˆCKD
AH=CK
=> ∆ AHB = ∆ CKD(c.g.c)
=> AB=CD.( 2 canh tương ứng)
tương tự ∆ CEB = ∆ AFD(c.g.c)
=> BC=AD.
b) ∆ABD và ∆CDB có:
AB=CD(CMT)
BC=AD(CMT)
BD chung.
=> ∆ABD=∆CDB(c.c .c)
=> ˆABD^=ˆCDB( 2 góc tương ứng)
=> AB // CD( hai góc so le trong bằng nhau)
CM
9 tháng 2 2019
ΔABD và ΔCDB có
AB = CD
AD = BC
BD cạnh chung
⇒ ΔABD = ΔCDB (c.c.c)
⇒ góc ABD = góc CDB (hai góc tương ứng)
Vậy AB // CD ( hai gó so le trong bằng nhau )
CM
9 tháng 1 2017
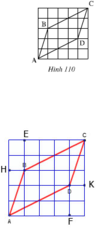
+ ΔAHB và ΔCKD có
HB = KD (=1)
góc AHB = góc CKD(=90º)
AH = CK (=3).
⇒ ΔAHB = ΔCKD(c.g.c)
⇒AB = CD (hai cạnh tương ứng)
+ ΔCEB và ΔAFD có
BE = DF (=2)
góc BEC = góc DFA (=90º)
CE = AF (=4).
⇒ ΔCEB = ΔAFD ( c.g.c)
⇒ BC = AD (hai cạnh tương ứng)
QD
20 tháng 4 2017
∆AHB và ∆ CKD có:
HB=KD.
AHB^=CKD^
AH=Ck
Nên ∆ AHB = ∆ CKD(c.g.c)
suy ra AB=CD.
tương tự ∆ CEB = ∆ AFD(c.g.c)
suy ra BC=AD.
b) ∆ABD và ∆CDB có:
AB=CD(câu a)
BC=AD(câu a)
BD chung.
Do đó ∆ABD=∆CDB(c.c .c)
Suy ra ˆABD=CDB^
Vậy AB // CD( hai góc so le trong bằng nhau)
Gọi giao điểm của đường kẻ ngang đi qua điểm A và đường kẻ dọc đi qua điểm B cắt nhau tại H.
Giao điểm đường kẻ ngang đi qua C và đường kẻ dọc đi qua D là K
Xét ΔAHB và ΔCKD, ta có:
AH = CK (bằng 2 ô vuông)
∠(AHB) =∠(CKD) =90o
BH = DK (bằng 3 ô vuông)
Suy ra ΔAHB= ΔCKD (c.g.c)
⇒ AB = CD (hai cạnh tương ứng) và ∠(BAH) =∠(DCK) (hai góc tương ứng)
Hai đường thẳng AB Và CD cắt đường thẳng AK có 2 góc ∠(BAH) và ∠(DCK) ̂ở vị trí đồng vị bằng nhau nên AB // CD.