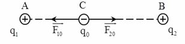
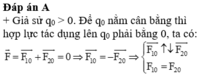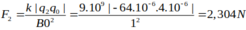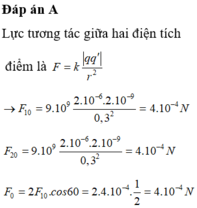Cho hai điện tích q 1 = 4 μC, q 2 = 9 μC đặt tại hai điểm A và B trong chân không. AB = 1 m. Xác định vị trí của điểm C để đặt tại C một điện tích q0 thì điện tích này nằm cân bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



![]()
Giả sử q 0 > 0. Để q0 cân bằng thì hợp lực tác dụng lên q 0 phải bằng không, ta có:
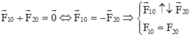
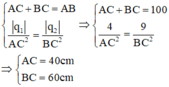
Vì q1; q2 cùng dấu nên C thuộc đoạn thẳng AB: AC + BC = AB (*) và q 1 A C 2 = q 2 B C 2 (**)
Từ (*) và (**) ta có:

Chọn: C
Hướng dẫn:
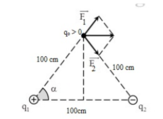
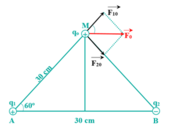
Tam giác ABM là tam giác đều cạnh a = 30 (cm) = 0,3 (m).
- Cường độ điện trường do q 1 = 2 . 10 - 2 (μC) = 2. 10 - 8 (C) đặt tại A, gây ra tại M là
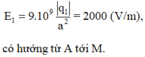
- Cường độ điện trường do q 2 = - 2 . 10 - 2 (μC) = - 2. 10 - 8 (C) đặt tại B, gây ra tại M là

- Cường độ điện trường tổng hợp tại điểm M là

- Lực điện tác dụng lên điện tích q 0 = 2 . 10 - 9 (C) đặt tại điểm M có hướng song song với AB và độ lớn là F = q 0 .E = 4. 10 - 6 (N).

Cường độ điện trường bằng 0 khi:
\(\begin{array}{l}\overrightarrow {{E_1}} + \overrightarrow {{E_2}} = \overrightarrow E = \overrightarrow 0 \Rightarrow \overrightarrow {{E_1}} = - \overrightarrow {{E_2}} \\ \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \\{E_1} = {E_2}\end{array} \right.\end{array}\)
Vì \(\left| {{q_1}} \right| < \left| {{q_2}} \right| \Rightarrow \)Điểm đó thuộc đường thẳng AB và ngoài đoạn AB, gần A hơn (r2>r1)
\(\begin{array}{l}\left\{ \begin{array}{l}{r_2} - {r_1} = AB\\\frac{{r_1^2}}{{r_2^2}} = \frac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}} = \frac{{\left| {{{3.10}^{ - 6}}} \right|}}{{\left| { - 3,{{5.10}^{ - 6}}} \right|}}\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}{r_1} = 3,6m\\{r_2} = 4,2m\end{array} \right.\end{array}\)
Vậy điểm cần tìm cách A 3,6 m và cách B 4,2 m