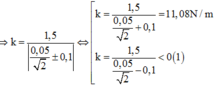
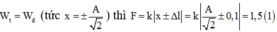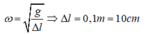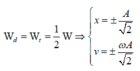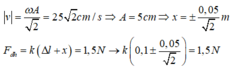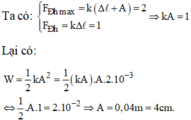Con lắc lò xo dao động điều hoà theo phương thẳng đứng, mốc thế năng ở vị trí cân bằng, khi thế năng bằng 1/8 động năng thì
A. . lực đàn hồi tác dụng lên vật có độ lớn bằng 1/3 lực đàn hồi cực đại
B. tốc độ của vật bằng 1/3 tốc độ cực đại
C. lực đàn hồi tác dụng lên vật có độ lớn bằng 1/9 lực đàn hồi cực đại
D. vật cách vị trí tốc độ bằng 0 một khoảng gần nhất là 2/3 biên độ