Cho hình chóp tứ giác S.ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Tỉ số là V S . M N P Q V S . A B C D là:
A. 1 8
B. 1 16
C. 3 8
D. 1 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
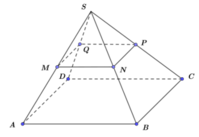
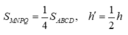
(với h’ và h lần lượt là khoảng cách từ S đến (MNPQ) và (ABCD)).
![]()
=> Chọn phương án A.

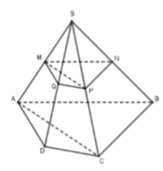
Xét tam giác SAB ta có: MN là đường trung bình suy ra MN // AB.
Tương tự ta có: NP // BC, PQ // CD, MQ // AD.
Mà ABCD là hình bình hành nên AB // CD, AD// CD, suy ra MN // PQ, MQ // NP.
Như vậy, MNPQ là hình bình hành.

Chọn đáp án B
Do S.ABCD là hình chóp tứ giác đều nên mỗi mặt bên là một tam giác cân tại đỉnh S.
Theo giả thiết ta có
![]()
Cắt hình chóp theo cạnh bên SA rồi trải các mặt bên thành một mặt phẳng ta được hình vẽ bên sao cho khí ghép lại thì A ≡ A '
Suy ra A S A ' ⏜ = 4 . A S B ⏜ = π 3 và ∆ S A A ' đều cạnh SA = a

Khi đó tổng AM + MN + NP + PQ là tổng của các đường gấp khúc.
Tổng này đạt nhỏ nhất bằng AQ nếu xảy ra trường hợp các điểm A, M, N, P, Q thẳng hàng.
Mà ∆ S A A ' đều có Q là trung điểm SA nên A Q = S A 3 2 = a 3 2
Vậy m i n A M + M N + N P + P Q = a 3 2

Chọn B.
Phương pháp
Sử dụng công thức tính tỉ số thể tích đối với khối chóp tam giác


Chú ý: Công thức tỉ số thể tích trên chỉ áp dụng đối với chóp tam giác.
Đáp án A
Theo công thức tỉ lệ tứ diện, ta có:
Theo dãy tỉ số bằng nhau ta có