Có bao nhiêu số tự nhiên có 4 chữ số khác nhau lấy từ tập T={1;2;3;...;9}
A. 126
B. 36
C. 3024
D. 5040
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A.
Cách 1: Lấy 4 chữ số khác nhau từ tập S rồi sắp xếp theo một thứ tự nào đó ta được một số tự nhiên.
Vậy số tự nhiên gồm 4 chữ số khác nhau lấy từ tập hợp S là một chỉnh hợp chập 4 của S.
Do đó số các số tự nhiên gồm 4 chữ số khác nhau lấy từ tập hợp S là A 6 4 = 360 (số).
Cách 2: Có 6 cách chọn chữ số hàng nghìn.
Khi đó có 5 cách chọn chữ số hàng trăm.
Khi đã chọn xong chữ số hàng nghìn và chữ số hàng tram thì có 44 cách chọn chữ số hàng chục
Cuốin ùng, khi đã chọn xong chữ số hang nghìn, hằng trăm, hàng chục thì còn 3 cách chọn chữ số hàng đơn vị.
Vậy các số tự nhiên gồm 4 chữ số khác nhau lấy từ tập hợp S là 6.5.4.3 = 360 (số).

1.
Chữ số hàng đơn vị có 4 cách chọn (từ 1,3,5,7)
Chọn và hoán vị 4 chữ số từ 6 chữ số còn lại: \(A_6^4\) cách
Tổng cộng: \(4.A_6^4\) cách
2.
Gọi chữ số cần lập có dạng \(\overline{abcd}\)
a.
Lập số có 4 chữ số bất kì (các chữ số đôi một khác nhau): \(A_6^4\) cách
Lập số có 4 chữ số sao cho số 0 đứng đầu: \(A_5^3\) cách
\(\Rightarrow A_6^4-A_5^3=300\) số
b.
Để số được lập là số chẵn \(\Rightarrow\) d chẵn
TH1: \(d=0\Rightarrow abc\) có \(A_5^3\) cách chọn
TH2: \(d\ne0\Rightarrow d\) có 2 cách chọn (từ 2;4)
a có 4 cách chọn (khác 0 và d), b có 4 cách chọn, c có 3 cách chọn
\(\Rightarrow2.4.4.3=96\) số
Tổng cộng: \(A_5^3+96=156\) số
Xác suất \(P=\dfrac{156}{300}=...\)

Không biết đề là ba số đầu khác 123 hay số đầu tiên khác 1, 2, 3. Đây t làm theo cách hiểu thứ nhất nha.
Theo giả thiết, số cách sắp xếp 3 chữ số đầu tiên là \(A_8^3-1=335\)
Số cách sắp xếp 2 chữ số cuối là \(A_5^2=20\)
\(\Rightarrow\) Có \(335.20=6700\) cách lập số tự nhiên thỏa mãn yêu cầu bài toán.
Không biết đúng không nữa-.-
Đáp án C.
Gọi số cần lập là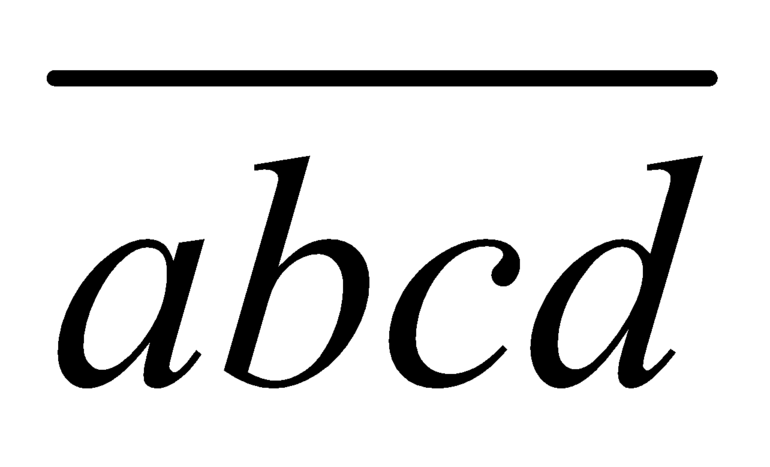 ;
; 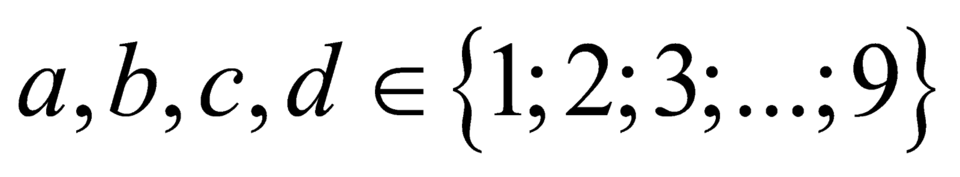 nên có
nên có 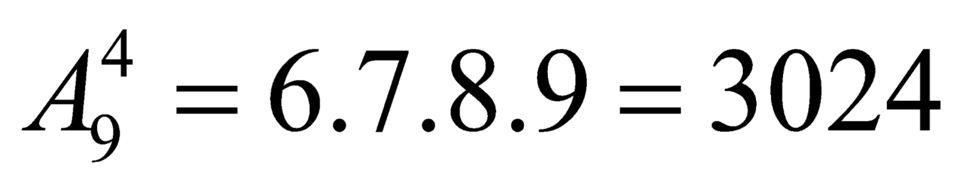 số.
số.