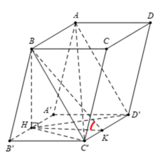
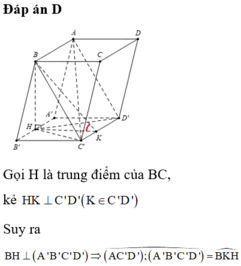
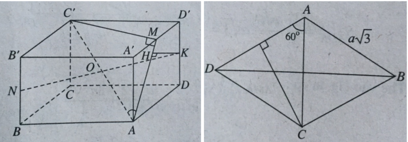
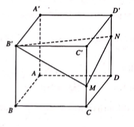
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là một hình thoi cạnh a, góc BAD= 60 o Gọi M là trung điểm AA' và N là trung điểm của CC' Chứng minh rằng bốn điểm B', M, N, D đồng phẳng. Hãy tính độ dài cạnh AA' theo a để tứ giác B'MDN là hình vuông.
A. a 2
B. a
C. a 2 2
D. a 3


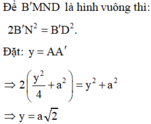


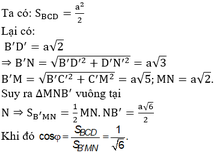
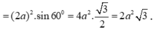
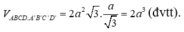
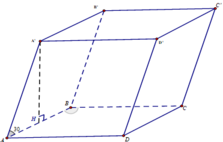
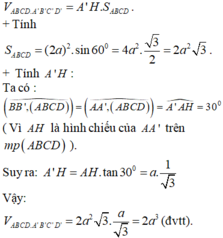
Đáp án A