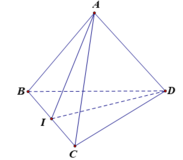
Cho tứ diện ABCD có hai mặt ABC và DBC là những tam giác đều cạnh bằng 1, A D = 2 . Gọi O là trung điểm cạnh AD. Xét hai khẳng định sau:
( I ) O là tâm mặt cầu ngoại tiếp tứ diện ABCD.
( I I ) O . A B C là hình chóp tam giác đều.
Hãy chọn khẳng định đúng
A. Chỉ (II) đúng
B. Cả (I) và (II) đều sai
C. Cả (I) và (II) đều đúng
D. Chỉ (I) đúng




Đáp án C
Ta có A D 2 = A B 2 + B D 2 = A C 2 + C D 2
⇒ Δ A B D , Δ A C D vuông cân tại B, C
Mà O là trung điểm cạnh A D ⇒ O A = O B − O C
⇒ O là tâm mặt cầu ngoại tiếp tứ diện ABCD.
Dễ thấy O A = O B − O C và Δ A B C đều cạnh a
⇒ khối chóp O . A B C là hình chóp tam giác đều