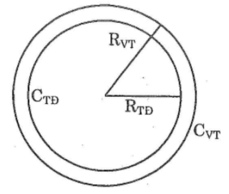
Đố vui: một kết quả bất ngờ. Biết rằng bán kính Trái đất: RTĐ ≈ 6370km (hình bên). Giả sử một chiếc vệ tinh bay vòng quanh Trái đất và cách mặt đất 100km.
Em hãy tính cụ thể và cho kết quả?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 6 2018
Vệ tinh cách mặt đất là 100km nên chu vi của vệ tinh quay một vòng hơn chu vi Trái đất một khoảng là: 2.3,14.100 = 628km < 1000km
A
27 tháng 6 2019
a) Vì vệ tinh cách mặt đất là 100km nên chu vi vệ tinh quay vòng hơn chu vi trái đất một khoảng 2.3,14.100 nên nhỏ hơn 1000km
b) Gọi bán kính của Trái Đất \(R_{TD}\), bán kính quỹ đạo vệ tinh \(R_{VT}\)
Chu vi trái đất \(2\pi R_{TD}\), chu vi quỹ đạo vệ tinh \(2\pi R_{VT}\)
Vì chu vi của đường tròn tỉ lệ thuận với bán kính nên ta có:
\(\frac{2\pi R_{VT}}{2\pi R_{TD}}=\frac{R_{VT}}{R_{TD}}\)
\(\Rightarrow\frac{2\pi R_{VT}-2\pi R_{TD}}{2\pi R_{TD}}=\frac{R_{VT}-R_{TD}}{R_{TD}}\)
\(\Rightarrow2\pi R_{VT}-2\pi R_{TD}=\frac{2\pi R_{TD}\left(R_{VT}-R_{TD}\right)}{R_{TD}}\)
\(\Rightarrow2\pi R_{VT}-2\pi R_{TD}=2\pi.100\approx628\left(km\right)\)
Quãng đường vệ tinh bay dài hơn chu vi trái đất khoảng 628km.
29 tháng 7 2017
Cần cách làm khác chứ cứ chụp sách giải rồi đăng lên thì làm chi cho mệt
27 tháng 6 2016
Gọi RTĐ và CTĐ là bán kính và chu vi Trái Đất :
RX và Cx là bán kính và chu vi của quỹ đạo vệ tinh (đường tròn mà vệ tinh bay một vòng).
vì chu vi và bán kính của đường tròn là hai đại lượng tỷ lệ thuận ,nên:
\(\frac{C_x}{C_{TĐ}}=\frac{R_x}{R_{TĐ}}\Rightarrow\frac{C_x-C_{TĐ}}{C_{TĐ}}=\frac{R_X-R_{TĐ}}{R_{TĐ}}\)
Hay Cx-CTĐ=(Rx-RTĐ).\(\frac{C_{TĐ}}{R_{TĐ}}=100\times2\pi\approx628km\)
Gọi bán kính của trái đất RTĐ, bán kính quỹ đạo vệ tinh RVT.
Chu vi trái đất 2πRTĐ, chu vi quỹ đạo vệ tinh 2πRVT. Ta cần tính 2πRVT - 2πRTD
Vì chu vi của đường tròn tỉ lệ với bán kính nên ta có:
Vậy quãng đường vệ tinh bay một vòng dài hơn chu vi trái đất khoảng 628 km.