Cho tam giác ABC, tia phân giác AD. Các tia phân giác ngoài tại đỉnh B và C cắt nhau ở E. Chứng minh ba điểm A, D, E thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ IH ⊥ AB, IJ ⊥ BC, IG ⊥ AC, KD ⊥ AB, KE ⊥ AC, KF ⊥ BC
Vì I nằm trên tia phân giác của ∠(BAC) nên IH = IG (tính chất tia phân giác)
Vì I nằm trên tia phân giác của ∠(BCA) nên IJ = IG (tính chất tia phân giác)
Suy ra: IH = IJ
Do đó I nằm trên tia phân giác của ∠(ABC) (1)
Vì K nằm trên tia phân giác của ∠(DAC) nên KD = KE (tính chất tia phân giác)
Vì K nằm trên tia phân giác của ∠(ACF) nên KE = KF (tính chất tia phân giác)
Suy ra: KD = KF
Do đó K nằm trên tia phân giác của ∠(ABC) (2)
Từ (1) và (2) suy ra: B, I, K thẳng hàng.

a: 1/2(góc A+góc B+góc C)=90 độ
góc ABK=1/2*góc ABx
=>góc ABK=1/2(góc A+góc C)
góc IBA=1/2*góc B
=>góc ABK+góc IBA=90 độ
=>BI vuông góc BK
b: góc BAK=180-120=60 độ
=>góc BAK=góc CAD=góc DAB=60 dộ
Kẻ tia Ay là tia đối của tia AD
=>góc yAK=góc CAD=60 độ
Xét ΔADB có
AK là tia phân giác góc ngoài của góc yAB
BK là phân giác ngoài của góc ABx
=>DK là phân giác của góc BDA

bài này dễ nhưng tạm thời chưa có thời gian để làm . Thông cảm

mình chỉ lm dc câu a thôi
đặt ABx là góc ngoài tam giác ABC ( thêm x vào, dòng này ko ghi vào vở)
a)vì AD là tia phân giác của góc A, CE là tia phân giác góc C nên
BO là tia phân giác góc B
=> góc ABO = 1/2 góc ABC (1)
vì BF là tia phân giác góc B nên:
góc FBA = 1/2 góc ABx (2)
cộng vế 1 và 2 vào ta có
góc ABO + góc FBA = 1/2 ( góc ABC + góc ABx)
góc FBO =1/2 * 180 độ
góc FBO = 90 độ
=> vuông

Lời giải:
Kẻ $KM, KT, KN$ lần lượt vuông góc với $AB, AC, BC$.
Vì $K$ thuộc tia phân giác $\widehat{MAC}$ nên $KM=KT$ (tính chất quen thuộc)
Vì $K$ thuộc tia phân giác $\widheat{ACN}$ nên $KN=KT$
$\Rightarrow KM=KN$
$\Rightarrow K$ thuộc tia phân giác $\widehat{MBN}$ hay $\widehat{ABC}$
Do đó $BI, BK$ cùng là tia phân giác $\widehat{ABC}$
$\Rightarrow B,I,K$ thẳng hàng
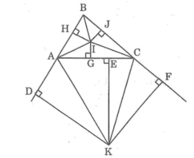
Gọi F,H,G lần lượt là hình chiếu vuông góc của điểm E xuống các đường thẳng AB, AC và BC.
Từ giả thiết suy ra EF = EG và EH = EG.
=> EF = EH nên E thuộc tia phân giác của góc BAC.
Mà AD là tia phân giác của góc BAC.
Vậy ba điểm A, D, E thẳng hàng.