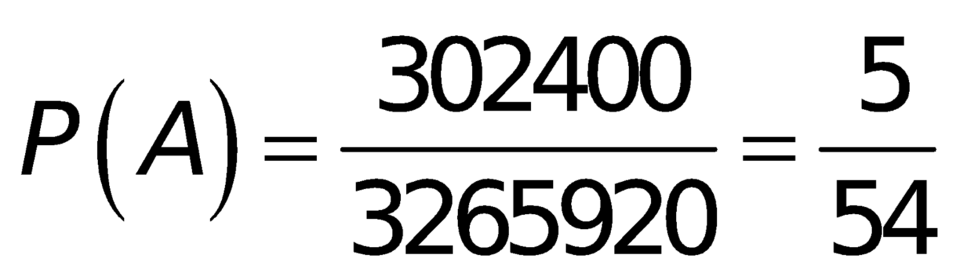Một danh sách số điện thoại thử nghiệm gồm 9 chữ số khác nhau. Hệ thống chọn ngẫu nhiên một số điện thoại để gắn vào sim. Xác suất để số được chọn có đúng 4 chữ số lẻ và chữ số 0 đứng giữa hai chữ số lẻ (các chữ số liền trước và liền sau của chữ số 0 là các chữ số lẻ) là: A. B. C. ...
Đọc tiếp
Một danh sách số điện thoại thử nghiệm gồm 9 chữ số khác nhau. Hệ thống chọn ngẫu nhiên một số điện thoại để gắn vào sim. Xác suất để số được chọn có đúng 4 chữ số lẻ và chữ số 0 đứng giữa hai chữ số lẻ (các chữ số liền trước và liền sau của chữ số 0 là các chữ số lẻ) là:
A. 
B. 
C. 
D. 
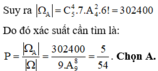
Đáp án C
Xét các số có 9 chữ số khác nhau:
- Có 9 cách chọn chữ số ở vị trí đầu tiên.
- Có
cách chọn 8 chữ số tiếp theo
Do đó số các số có 9 chữ số khác nhau là: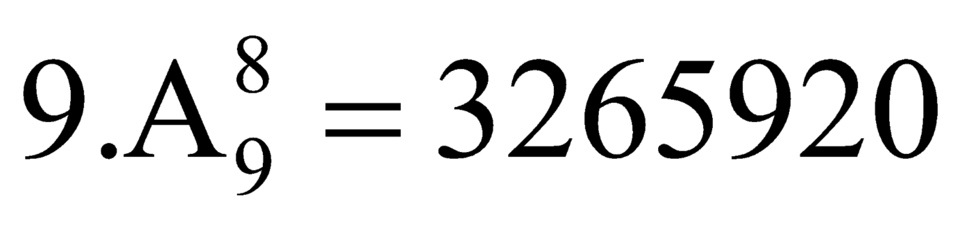
Xét các số thỏa mãn đề bài:
- Có
cách chọn 4 chữ số lẻ.
- Đầu tiên ta xếp vị trí cho chữ số 0, do chữ số 0 không thể đứng đầu và cuối nên có 7 cách xếp.
- Tiếp theo ta có
cách chọn và xếp hai chữ số lẻ đứng hai bên chữ số 0.
- Cuối cùng ta có 6! cách xếp 6 chữ số còn lại vào 6 vị trí còn lại.
Gọi A là biến cố đã cho, khi đó
Vậy xác suất cần tìm là