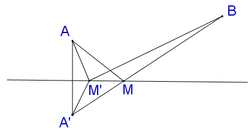
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
P
:
x
+
y
+
z
+
1
=
0.
Một phần tử chuyển động thẳng với vận tốc không đổi từ
A
(
1
;
-
3
;
0
)
đến gặp mặt phẳng (P) tại M , sau đó phần tử đó tiếp tục chuyển động thẳng từ M đến
B
(
2
;
1
;
−
6
)
cùng với vận tốc như lúc trước. Tìm hoành...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng P : x + y + z + 1 = 0. Một phần tử chuyển động thẳng với vận tốc không đổi từ A ( 1 ; - 3 ; 0 ) đến gặp mặt phẳng (P) tại M , sau đó phần tử đó tiếp tục chuyển động thẳng từ M đến B ( 2 ; 1 ; − 6 ) cùng với vận tốc như lúc trước. Tìm hoành độ của M sao cho thời gian phần tử chuyển động từ A qua M đến B là ít nhất
A. 4 3
B. 5 3
C. − 1 3
D. − 1
suy ra tọa độ điểm M là nghiệm của hệ phương trình
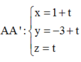
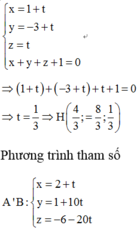
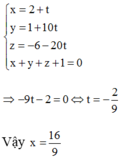
Đáp án C
Xét mặt phẳng P : x + y + z + 1 = 0.
Đặt f x ; y ; z = x + y + z + 1
Ta có f A = − 1 ; f B = − 2 suy ra f A . f B > 0 ⇒ A , B cùng phía so với P
Gọi C là điểm đối xứng của A qua mặt phẳng P ⇒ A C ⊥ P
Phương trình đường thẳng AC có u → = 1 ; 1 ; 1 và đi qua A là x − 1 1 = y + 3 1 = z 1
Điểm:
C ∈ A C ⇒ C t + 1 ; t − 3 ; t ∈ P ⇒ t + 1 + t − 3 + t + 1 = 0 ⇔ t = 1 3 ⇒ C 4 3 ; − 8 3 ; 1 3
Lại có
A M + B M = C M + B M ⇒ C M + B M min ⇔ B , C . M t h ẳ n g h à n g
Phương trình đường thẳng BC là x − 2 2 = y − 1 11 = z + 6 − 19
Điểm:
M ∈ B C ⇒ M 2 m + 2 ; 11 m + 1 ; − 19 m − 6
Mặt khác:
M = B C ∩ P ⇒ 2 m + 2 + 11 m + 1 − 19 m − 6 + 1 = 0 ⇔ m = − 1 3