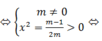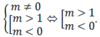Có tất cả bao nhiêu giá trị thực của tham số m để đồ thị của hàm số y = x 4 - 2 m 2 + 2 có ba điểm cực trị cùng với điểm D(2;1) tạo thành một tứ giác nội tiếp được đường tròn?
A. 0
B. 2
C. 3.
D. 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn D
Ta có y ' = 3 x 2 - 6 m x + m - 1
Hàm số có cực đại, cực tiểu khi và chỉ khi PT y ' = 0 có hai nghiệm phân biệt
Điều này tương đương
![]()
Hai điểm cực trị có hoành độ dương
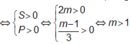
Vậy các giá trị cần tìm của m là m >1

Để hàm số có ba điểm cực trị khi và chỉ khi ab< 0 hay 1.( -2m) <0
Suy ra m> 0
Khi đó
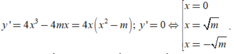
Suy ra tọa độ các điểm cực trị của đồ thị hàm số là:
A 0 ; 2 , B m ; - m 2 + 2 , C - m ; - m 2 + 2
Ycbt O A . O B . O C = 12 ⇔ 2 m + - m 2 + 2 2 = 12
Giải ra ta được m=2; có một giá trị nguyên.
Chọn B.

Chọn đáp án C
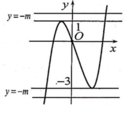
Dựa vào đồ thị ta thấy đồ thị hàm số y = f(x) có 2 điểm cực trị.
Để đồ thị hàm số y = f x + m có 3 điểm cực trị thì đường thẳng y= -m cắt đồ thị y = f(x) tại 1 điểm duy nhất.
(Không tính điểm cực trị của đồ thị hàm số y = f(x))
Dựa vào đồ thị:
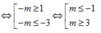

Đáp án D
Ta có y’ = 4mx3 – 2(m – 1)x.
y' = 0 ó 4mx3 – 2(m – 1)x = 0 ó
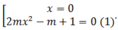
Để hàm số có 3 điểm cực trị