Giải các bất phương trình sau bằng 1 2 x < x - 1 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 7x+35=0
=>7x=-35
=>x=-5
b: \(\dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\)
=>8-x-8(x-7)=1
=>8-x-8x+56=1
=>-9x+64=1
=>-9x=-63
hay x=7(loại)
a, \(7x=-35\Leftrightarrow x=-5\)
b, đk : x khác 7
\(8-x-8x+56=1\Leftrightarrow-9x=-63\Leftrightarrow x=7\left(ktm\right)\)
vậy pt vô nghiệm
2, thiếu đề


\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)

x^2( - 2) - 9x = - 18
<=>-2x2-9x=-18
=>-2x2-9x+18=0
(-9)2-(-4(2.18))=225
\(x_{1,2}=\frac{-b\pm\sqrt{\Delta}}{2a}=-\frac{9\pm\sqrt{225}}{4}\)
x1=-6;x2=\(\frac{3}{2}\)
\(a.\) \(x^2\left(-2\right)-9x=-18\)
\(\Leftrightarrow\) \(2x^2+9x=18\)
\(\Leftrightarrow\) \(2x^2+9x-18=0\)
\(\Leftrightarrow\) \(2x^2-3x+12x-18=0\)
\(\Leftrightarrow\) \(x\left(2x-3\right)+6\left(2x-3\right)=0\)
\(\Leftrightarrow\) \(\left(2x-3\right)\left(x+6\right)=0\)
\(\Leftrightarrow\) \(2x-3=0\) hoặc \(x+6=0\)
\(\Leftrightarrow\) \(x=\frac{3}{2}\) hoặc \(x=-6\)
Vậy, tập nghiệm của pt trên là \(S=\left\{-6;\frac{3}{2}\right\}\)
\(b.\)
Điều kiện để phương trình có nghĩa là \(x\ne\frac{1}{2}\)
Với điều kiện trên thì phương trình đã cho tương đương với:
\(\frac{7}{1-2x}\le0\) \(\Leftrightarrow\) \(1-2x\le0\) \(\Leftrightarrow\) \(1\le2x\) \(\Leftrightarrow\) \(x\ge\frac{1}{2}\)
Để thỏa mãn điều kiện xác định thì \(x>\frac{1}{2}\) (vì khi \(x=\frac{1}{2}\) thì mẫu thức bằng \(0\) nên phương trình không thể thực hiện được)
Kết luận: \(S=\left\{x\in R\text{|}x>\frac{1}{2}\right\}\)

Vẽ đồ thị của hàm số 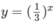 và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
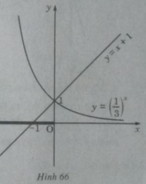
Khi x < 0 đồ thị của hàm số 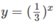 nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là (-
∞
;0]
nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là (-
∞
;0]

1:
ĐKXĐ: x<>3
\(\dfrac{x-1}{x-3}>1\)
=>\(\dfrac{x-1-\left(x-3\right)}{x-3}>0\)
=>\(\dfrac{x-1-x+3}{x-3}>0\)
=>\(\dfrac{2}{x-3}>0\)
=>x-3>0
=>x>3
2: ĐKXĐ: \(\left[{}\begin{matrix}x>=3\\x< =-4\end{matrix}\right.\)
\(\sqrt{x^2+x-12}< 8-x\)
=>\(\left\{{}\begin{matrix}8-x>=0\\x^2+x-12< \left(8-x\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =8\\x^2+x-12-x^2+16x-64< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =8\\17x-76< 0\end{matrix}\right.\)
=>\(x< \dfrac{76}{17}\)
Kết hợp ĐKXĐ, ta được: \(\left[{}\begin{matrix}3< =x< \dfrac{76}{17}\\x< =-4\end{matrix}\right.\)

1) \(ĐK:x\ne2\)
Nếu \(x>2\)
BPT ⇔ \(x^2-2x+5-\left(x-1\right)\left(x-2\right)\ge0\) ⇔ \(x^2-2x+5-\left(x^2-3x+3\right)\ge0\)
⇔\(x+2\ge0\) ⇔\(x\ge-2\) ⇒ Lấy \(x\ge2\)
Nếu \(x< 2\)
BPT ⇔\(\dfrac{-\left(x^2-2x+5\right)}{x-2}-x+1\ge0\) ⇔\(-x^2+2x-5-\left(x-1\right)\left(x-2\right)\ge0\)
⇔\(-x^2+2x-5-x^2+3x-2\ge0\)
⇔\(-2x^2+5x-7\ge0\)
⇔\(x^2-\dfrac{5}{2}x+\dfrac{7}{2}\le0\)
⇔\(\left(x-\dfrac{5}{4}\right)^2\le\dfrac{11}{4}\)
⇔\(\left[{}\begin{matrix}x-\dfrac{5}{4}\le\dfrac{11}{4}\\x-\dfrac{5}{4}\le\dfrac{-11}{4}\end{matrix}\right.\) ⇔\(\left[{}\begin{matrix}x\le4\\x\le\dfrac{-3}{2}\end{matrix}\right.\) ⇔ \(x\le\dfrac{-3}{2}\)
S= [2;+∞)U(-∞;\(\dfrac{-3}{2}\)]
2) \(ĐK:x\ne-1\)
Nếu \(x>-1\)
BPT ⇔ \(2x-3-2\left(x+1\right)< 0\) ⇔\(2x-3-2x-2< 0\)
⇔\(-5< 0\) ( luôn đúng với mọi \(x>-1\))
Nếu \(x< -1\)
BPT⇔\(\dfrac{-\left(2x-3\right)}{x+1}-2< 0\) ⇔\(-\left(2x-3\right)-2\left(x+1\right)< 0\) ⇔\(-4x+1< 0\) ⇔ \(x>\dfrac{-1}{4}\)
Vậy S=....

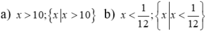
Vẽ đồ thị của hàm số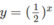 và đường thẳng
và đường thẳng 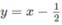 trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số
trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số 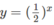 nằm phía dưới đường thẳng
nằm phía dưới đường thẳng 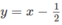 . Vậy tập nghiệm của bất phương trình đã cho là (1;+
∞
)
. Vậy tập nghiệm của bất phương trình đã cho là (1;+
∞
)