So sánh 9920 và 999910
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



`99^{20}=(99^{2})^{10}=(99.99)^{10}`
`9999^{10}=(99.101)^{10}`
Vì `(99.99)^{10}<(99.101)^{10}`
`->99^{20}<9999^{10}`
Ta có: \(99^{20}=\left(99^2\right)^{10}=9801^{10}\)
mà 9801<9999
nên \(99^{20}< 9999^{10}\)

Lời giải:
a) $A-B=99.10^k-10^{k+2}-10^k=99.10^k-100.10^k-10^k$
$=10^k(99-100-1)=-2.10^k< 0$
$\Rightarrow A<b$
b) $99^{20}-9999^{10}=99^{20}-(99.101)^{10}$
$<99^{20}-(99.99)^{10}=99^{20}-99^{20}=0$
$\Rightarrow 99^{20}<9999^{10}$

a) \(2^{300}=\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}>8^{100}\)
\(\Rightarrow2^{300}< 3^{200}\)
b) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\Rightarrow99^{20}< 9999^{10}\)
c) \(3^{500}=\left(3^5\right)^{100}=243^{100}\)
\(7^{300}=\left(7^3\right)^{100}=343^{100}>243^{100}\)
\(\Rightarrow3^{500}< 7^{300}\)

\(1,\\ a,2^x=16=2^4\Rightarrow x=4\\ b,3^{x+1}=9^x=3^{2x}\\ \Rightarrow x+1=2x\Rightarrow x=1\\ c,2^{3x+2}=4^{x+5}=2^{2\left(x+5\right)}\\ \Rightarrow3x+2=2x+10\Rightarrow x=8\\ d,3^{2x-1}=243=3^5\\ \Rightarrow2x-1=5\Rightarrow x=3\\ 2,\\ a,2^{225}=8^{75}< 9^{75}=3^{150}\\ b,2^{91}=\left(2^{13}\right)^7=8192^7>3125^7=\left(5^5\right)^7=5^{35}\\ c,99^{20}=\left(99^2\right)^{10}< \left(99\cdot101\right)^{10}=9999^{10}\\ 3,\\ a,12^8\cdot9^{12}=2^{16}\cdot3^8\cdot3^{24}=2^{16}\cdot3^{32}=\left(2\cdot3^2\right)^{16}=18^{16}\\ b,75^{20}=\left(3\cdot5^2\right)^{20}=3^{20}\cdot5^{40}=\left(3^{20}\cdot5^{10}\right)\cdot5^{30}=\left(3^2\cdot5\right)^{10}\cdot5^{30}=45^{10}\cdot5^{30}\)
Bài 1:
a) \(\Rightarrow2^x=2^4\Rightarrow x=4\)
b) \(\Rightarrow3^{x+1}=3^{2x}\Rightarrow x+1=2x\Rightarrow x=1\)
c) \(\Rightarrow2^{3x+2}=2^{2x+10}\Rightarrow3x+2=2x+10\Rightarrow x=8\)
d) \(\Rightarrow3^{2x-1}=3^5\Rightarrow2x-1=5\Rightarrow x=3\)
Bài 2:
a) \(2^{225}=\left(2^3\right)^{75}=8^{75}< 9^{75}=\left(3^2\right)^{75}=3^{150}\)
b) \(2^{91}=\left(2^{13}\right)^7=8192^7>3125^7=\left(5^5\right)^7=5^{35}\)
c) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\)
Bài 3:
a) \(12^8.9^{12}=\left(4.3\right)^8.9^{12}=4^8.3^8.9^{12}=2^{16}.9^4.9^{12}=2^{16}.9^{16}=\left(2.9\right)^{16}=18^{16}\)
b) \(75^{20}=\left(75^2\right)^{10}=5625^{10}=\left(45.125\right)^{10}=45^{10}.125^{10}=45^{10}.5^{30}\)

a: \(45^{10}\cdot5^{30}=45^{10}\cdot\left(5^3\right)^{10}\)
\(=\left(45\cdot5^3\right)^{10}=\left(3^2\cdot5^4\right)^{10}=3^{20}\cdot5^{40}\)
\(75^{19}=\left(5^2\cdot3\right)^{19}=5^{38}\cdot3^{19}\)
\(\frac{45^{10}\cdot5^{30}}{75^{19}}=\frac{3^{20}\cdot5^{40}}{5^{38}\cdot3^{19}}=5^2\cdot3=75>1\)
Do đó: \(45^{10}\cdot5^{30}>75^{19}\)
=>Đúng
b: Đúng
c: \(99^{20}=\left(99^2\right)^{10}=9801^{10}<9999^{10}\)
=>Sai

Bài 8:
a) \(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{150}=\left(3^2\right)^{75}=9^{75}\)
Vì \(8^{75}< 9^{75}\Rightarrow2^{225}< 3^{150}\)
b) \(2^{91}=\left(2^{13}\right)^7=8192^7\)
\(5^{35}=\left(5^5\right)^7=3125^7\)
Vì \(8192^7>3125^7\Rightarrow2^{91}>5^{35}\)
c) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\)

a: \(2^{300}=8^{100}\)
\(3^{200}=9^{100}\)
mà 8<9
nên \(2^{300}< 3^{200}\)
b: \(3^{500}=243^{100}\)
\(7^{300}=343^{100}\)
mà 243<243
nên \(3^{500}< 7^{300}\)
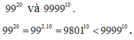


Ta có: 9920 = (992)10= 980110
9801 < 9999 => 980110 < 999910
Vậy 9920 < 999910