Cho hàm số: g ( x ) = - 2 x 3 - 3 x + 5 . Tính g(3)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()

c: Ở hai hàm số trên, nếu lấy biến x cùng một giá trị thì f(x) sẽ nhỏ hơn g(x) 3 đơn vị

\(a,f\left(-2\right)=\dfrac{3}{4}\left(-2\right)=-\dfrac{3}{2}\\ f\left(0\right)=\dfrac{3}{4}\cdot0=0\\ f\left(1\right)=\dfrac{3}{4}\cdot1=\dfrac{3}{4}\\ b,g\left(-2\right)=\dfrac{3}{4}\left(-2\right)+3=-\dfrac{3}{2}+3=\dfrac{3}{2}\\ g\left(0\right)=\dfrac{3}{4}\cdot0+3=3\\ g\left(1\right)=\dfrac{3}{4}\cdot1+3=\dfrac{15}{4}\)

a: Thay x=3 và y=-42 vào y=ax, ta được:
3a=-42
hay a=-14

a) Ta có:
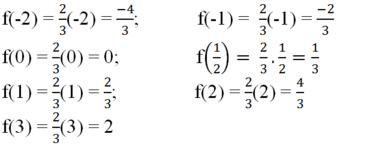
b) Ta có:
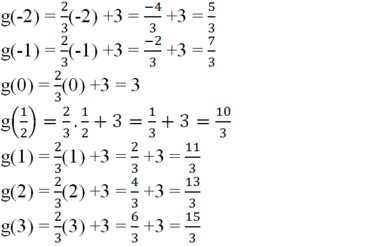
c) Từ kết quả câu a, b ta được bảng sau:

Nhận xét:
- Hai hàm số
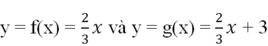
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.

a: \(F\left(3\right)=3\left(3-2\right)=3\cdot1=3\)
\(\left[F\left(\dfrac{2}{3}\right)\right]^2=\left[\dfrac{2}{3}\cdot\left(\dfrac{2}{3}-2\right)\right]^2\)
\(=\left[\dfrac{2}{3}\cdot\dfrac{-4}{3}\right]^2=\left(-\dfrac{8}{9}\right)^2=\dfrac{64}{81}\)
\(G\left(-\dfrac{1}{2}\right)=-\left(-\dfrac{1}{2}\right)+6=6+\dfrac{1}{2}=\dfrac{13}{2}\)
b: F(x)=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
c: F(a)=G(a)
=>\(a\left(a-2\right)=-a+6\)
=>\(a^2-2a+a-6=0\)
=>\(a^2-a-6=0\)
=>(a-3)(a+2)=0
=>\(\left[{}\begin{matrix}a-3=0\\a+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=3\\a=-2\end{matrix}\right.\)

Ta có
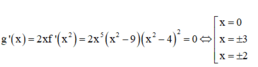
Bảng biến thiên của hàm số y= g( x)
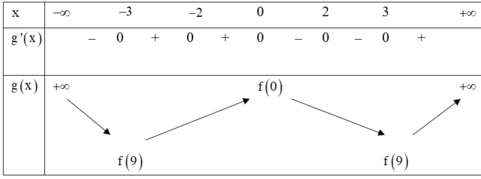
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( 3: + ∞) hàm số nghịch biến trong khoảng (-∞; -3) .
Hàm số có 3 cực trị, hàm số đạt giá trị nhỏ nhất tại x= ±3
Vậy có 3 khẳng định đúng là khẳng định I, II, IV
Chọn C.

