Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

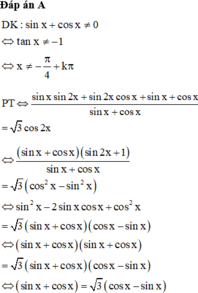
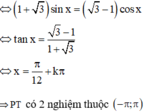

Chọn C
Ta có: ![]() nên (1) và (2) có nghiệm.
nên (1) và (2) có nghiệm.
Cách 1:
Xét: ![]()
![]() nên (3) vô nghiệm.
nên (3) vô nghiệm.
Cách 2:
Điều kiện có nghiệm của phương trình: sin x + cos x = 2 là: 
(vô lý) nên (3) vô nghiệm.
Cách 3:
Vì 

nên (3) vô nghiệm.

\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x+\dfrac{1}{2}sin\left(4x-\dfrac{\pi}{2}\right)+\dfrac{1}{2}sin2x-\dfrac{3}{2}=0\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^22x-\dfrac{1}{2}cos4x+\dfrac{1}{2}sin2x-\dfrac{3}{2}=0\)
\(\Leftrightarrow1-\dfrac{1}{2}\left(\dfrac{1-cos4x}{2}\right)-\dfrac{1}{2}cos4x+\dfrac{1}{2}sin2x-\dfrac{3}{2}=0\)
\(\Leftrightarrow-\dfrac{3}{4}-\dfrac{1}{4}cos4x+\dfrac{1}{2}sin2x=0\)
\(\Leftrightarrow-\dfrac{3}{4}-\dfrac{1}{4}\left(1-2sin^22x\right)+\dfrac{1}{2}sin2x=0\)
\(\Leftrightarrow...\)

Với \(cosx=0\) ko phải nghiệm
Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)
\(\Rightarrow tan^2x-4\sqrt{3}tanx+1=-2\left(1+tan^2x\right)\)
\(\Leftrightarrow3tan^2x-4\sqrt{3}tanx+3=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=\sqrt{3}\\tanx=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\\x=\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)

Đáp án C
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
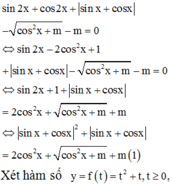
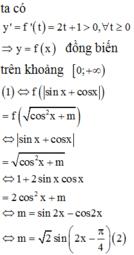

Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài.