Tập nghiệm của phương trình 3 tan x / 4 = 3 trong khoảng [0;2π) là:
A. {2π/3}
B. {3π/2}
C. {π/3; 2π/3}
D. {π/2; 3π/2}
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(f\left(x\right)=x^4+3x^3+x-1\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên R
\(f\left(-1\right)=-4< 0\) ; \(f\left(3\right)=164>0\)
\(\Rightarrow f\left(-1\right).f\left(3\right)< 0\Rightarrow f\left(x\right)\) có nghiệm trong khoảng (-1;3)

Chọn B.
Phương pháp:
Đưa phương trình về dạng tích, giải phương trình tìm nghiệm và tìm điều kiện để bài toán thỏa.
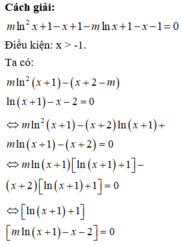
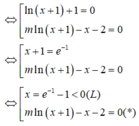

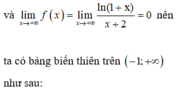
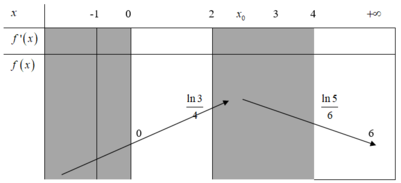



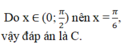
Chú ý: Chúng ta có thể loại ngay phương án D vì 5π/6 ∉ [0; π/2 ] và thay bởi việc giải bài toán như trên, chúng ta có thể sử dụng máy tính để kiểm tra 2 trong số 3 phương án còn lại để xác định đáp án của bài toán.

+) Thay x = 5 vào phương trình 2 x − 3 = x + 2 x − 4 ta được
2.5 − 3 = 5 + 2 5 − 4 ⇔ 7 = 7 1 = 7
Vậy 5 là nghiệm của phương trình 2 x − 3 = x + 2 x − 4 khẳng định (I) đúng.
+) Tập nghiệm của phương trình 7 – x = 2x – 8 là x = 5 là khẳng định sai vì kết luận x = 5 không phải là tập nghiệm.
+) Ta có: 10 - 2x = 0 ⇔ 2x = 10 ⇔ x = 5
Vậy tập nghiệm của phương trình là S = {5}.
Do đó khẳng định (III) là đúng.
Vậy có hai mệnh đề đúng.
Đáp án cần chọn là: C

Ta có:
\({x^2} - 2x - 3 = 0 \Leftrightarrow (x + 1)(x - 3) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right. \Rightarrow E = \{ - 1;3\} \)
Lại có: \((x + 1)(2x - 3) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \frac{3}{2}\end{array} \right.\)
\( \Rightarrow G = \left\{ { - 1;\frac{3}{2}} \right\}\)
\( \Rightarrow P = E \cap G = \left\{ { - 1} \right\}\).
Xét phương trình \(x^2-2x-3=0\) có: \(a-b+c=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{c}{a}=3\end{matrix}\right.\Rightarrow E=\left\{-1;3\right\}.\)
Xét phương trình \(\left(x+1\right)\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+1=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{2}\end{matrix}\right.\Rightarrow G=\left\{-1;\dfrac{3}{2}\right\}.\)
\(\Rightarrow P=E\cap G=\left\{-1\right\}.\)
Chọn A