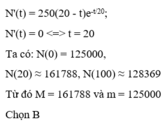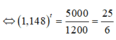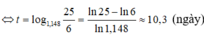Giả sử số lượng cá thể trong một mẻ cấy vi khuẩn thay đổi theo thời gian t theo công thức N ( t ) = 5000 25 + t e t 20
Tìm số lượng cá thể vi khuẩn lớn nhất (kí hiệu M) và nhỏ nhất (kí hiệu m) của mẻ cấy này trong khoảng thời gian 0 ≤ t ≤ 100
A. M = 161788, m = 128369
B. M = 161788, m = 125000
C. M = 225000, m = 125000
D. M = 225000, m = 128369