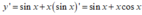Đạo hàm của hàm số y = xsinx bằng
A. y' = sinx-xcosx
B. y' = sinx + xcosx
C. y' = xcosx
D. y' = -xcosx
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
18 tháng 4 2021
\(y'=\left(\sin^4x\right)'\cos x+\sin^4x\left(\cos x\right)'=4\sin^3x.\cos^2x-\sin^5x\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2021
\(y'=4sin^3x.cosx.cosx-sinx.sin^4x=4sin^3x.cos^2x-sin^5x\)
CM
26 tháng 6 2019
Ta có ∫ (xcosx)’dx = (xcosx) và ∫ cosxdx = sinx. Từ đó
∫ xsinxdx = - ∫ [(xcosx)’ – cosx]dx = -∫ (xcosx)’dx + ∫ cosxdx = - xcosx + sinx + C.
CM
12 tháng 8 2018
Do F(x) là một nguyên hàm của hàm số f(x) nên F ' x = f x , ∀ x ∈ R
⇔ a + d cos x + c x cos x + c - b sin x - a x sin x = cos x , ∀ x ∈ R ⇔ c + d = 0 c = 1 c - b = 0 a = 0 ⇔ a = d = 0 b = c = 1
Đáp án B
CM
9 tháng 1 2019
Đáp án B
Đặt:
u = x d v = cos x d x ⇔ d u = d x v = sin x ⇒ ∫ x cos x d x = x sin x − ∫ sin x d x = x sin x + cos x + C
CM
16 tháng 11 2019
Chọn A
Đặt u = x , d v = cos x d x
Suy ra d u = d x , v = sin x
Do đó I = x sin x + ∫ sin x d x = x sin x - cos x + C
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 10 2020
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^3x\)
\(\Leftrightarrow1+\frac{sinx}{cosx}.\frac{1}{cos^2x}-3tan^2x=0\)
\(\Leftrightarrow1+tanx\left(1+tan^2x\right)-3tan^2x=0\)
\(\Leftrightarrow tan^3x-3tan^2x+tanx+1=0\)
\(\Leftrightarrow\left(tanx-1\right)\left(tan^2x-2tanx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=1-\sqrt{2}\\tanx=1+\sqrt{2}\end{matrix}\right.\) \(\Leftrightarrow...\)
CM
18 tháng 7 2018
Chọn đáp án A
Ta F x = x cos x là một nguyên hàm của hàm số f x nên suy ra
Đáp án B
Ta có: