Cho hàm số y = tanx – cotx. Khoảng mà hàm số xác định là:
A. 0 ; 2 π \ π 2
B. 0 ; 2 π
C. 0 ; 2 π \ 3 π 2
D. 0 ; 2 π \ π 2 ; π ; 3 π 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .

Ta có tập xác định của hàm số \(y=cosx\) là \(\mathbb{R}.\)
Nếu với \(x\in\mathbb{R}\) thì \(-x\in\mathbb{R}\) và\(y\left(-x\right)=cos\left(-x\right)=cosx=y\left(x\right).\)
Vậy hàm số \(y=cosx\) là hàm số chẵn.
\(\Rightarrow B\)

a) Hàm số y = tanx nhận giá trị bằng – 1
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = tanx và y = - 1
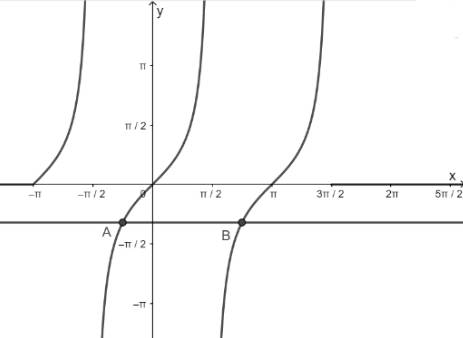
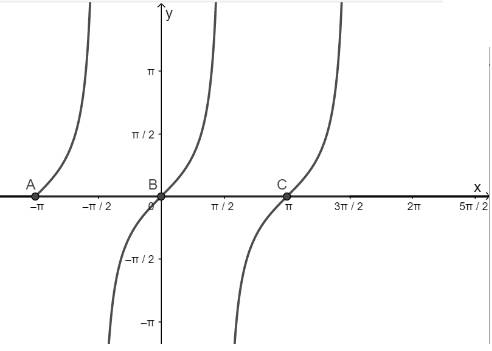
b) Hàm số y = tanx nhận giá trị bằng 0
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
c) Hàm số y = cotx nhận giá trị bằng 1
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = cotx và y = 1
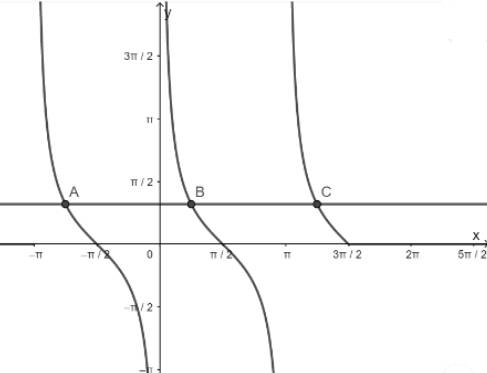
d) Hàm số y = cotx nhận giá trị bằng 0
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
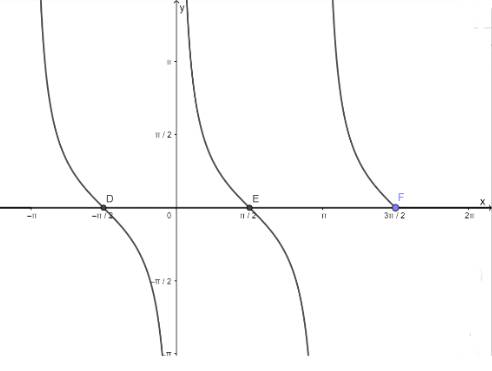

Chọn B
y ' = 1 cos 2 x + 1 sin 2 x = sin 2 x + cos 2 x sin 2 x . cos 2 x = 1 ( s inx. cosx) 2 = 1 sin 2 x 2 2 = 4 sin 2 2 x

a) Do hoành độ giao điểm nằm trên khoảng \(\left( {0;\pi } \right)\) nên: \(\cot x = m \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \)
b) Nhận xét: trên khoảng\(\left( {0;\pi } \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha + k\pi \)
Chọn D