Giải bất phương trình l o g ( x 2 - 2 x

PT

Pham Trong Bach

15 tháng 1 2018

Giải bất phương trình l o g ( x 2 - 2 x - 2 ) ≤ 0 A. [-1; 3] B. ( 1 - 3 ; 1 + 3 ) C. [ - 1 ; 1 - 3 ) ∪ ( 1 + 3 ; 3 ] D. (-∞; -1) ∪ (3;...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

15 tháng 1 2018

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

⇒ [ - 1 ; 1 - 3 ) ∪ ( 1 + 3 ; 3 ]

Chọn C

Đúng(0)

NP

Nguyễn Phương Thùy

11 tháng 9 2021

cho hàm số $f\left(x\right)=x^3-3x^2+2$

a, giải bất phương trình $f'\left(x\right)\le0$

b, giải phương trình $f'=\left(x^2-3x+2\right)=0$

c, đặt $g\left(x\right)=f\left(1-2x\right)+x^2-x+2022$ giải bất phương trình$g'\left(x\right)\ge0$

#Toán lớp 11

2

NH

Nguyễn Hoàng Minh

11 tháng 9 2021

$a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2$

Đúng(2)

AH

Akai Haruma

Giáo viên

11 tháng 9 2021

Lời giải:

a. $f'(x)\leq 0$

$\Leftrightarrow 3x^2-6x\leq 0$

$\Leftrightarrow x(x-2)\leq 0$

$\Leftrightarrow 0\leq x\leq 2$

b.

$f'(x)=x^2-3x+2=0$

$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$

$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$

$\Leftrightarrow x-2=0$

$\Leftrightarrow x=2$

c.

$g(x)=f(1-2x)+x^2-x+2022$

$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$

$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$

$g'(x)\geq 0$

$\Leftrightarrow -24x^2+2x+5\geq 0$

$\Leftrightarrow (5-12x)(2x-1)\geq 0$

$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$

Đúng(1)

PT

Pham Trong Bach

3 tháng 6 2019

Giải bất phương trình g ' ( x ) ≤ 0 với g ( x ) = x 2 + 3 x − 9 x − 2 A. S = (1; 3) B. S = 1 ; 3 / 2 C. S = − ∞ ; 1 ∪ ( 3 ; + ∞ ) D. S = ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

3 tháng 6 2019

Ta có

g ' ( x ) = ( 2 x + 3 ) . ( x − 2 ) − 1. ( x 2 + 3 x − 9 ) ( x − 2 ) 2 = x 2 − 4 x + 3 ( x − 2 ) 2

Mà g ' ( x ) ≤ 0

⇔ x 2 − 4 x + 3 ≤ 0 x − 2 ≠ 0 ⇔ 1 ≤ x ≤ 3 x ≠ 2 ⇔ x ∈ 1 ; 3 \ 2

Vậy tập nghiệm bất phương trình là: S=[1 ; 3]\{2}

Chọn đáp án B

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

23 tháng 9 2023

Giải các bất phương trình sau:

a) $2{x^2} + 3x + 1 \ge 0$

b) $ - 3{x^2} + x + 1 > 0$

c) $4{x^2} + 4x + 1 \ge 0$

d) $ - 16{x^2} + 8x - 1 < 0$

e) $2{x^2} + x + 3 < 0$

g) $ - 3{x^2} + 4x - 5 < 0$

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

23 tháng 9 2023

a) $2{x^2} + 3x + 1 \ge 0$

Tam thức bậc hai $f\left( x \right) = 2{x^2} + 3x + 1$ có 2 nghiệm phân biệt $x = - 1,x = \frac{{ - 1}}{2}$

hệ số $a = 2 > 0$

Ta có bảng xét dấu f(x) như sau:

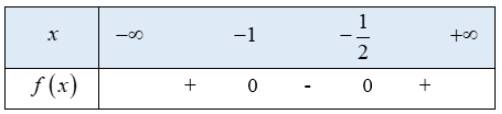
Từ bảng xét dấu ta thấy $f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.$

Vậy tập nghiệm của bất phương trình là $\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)$

b) $ - 3{x^2} + x + 1 > 0$

Tam thức bậc hai $f\left( x \right) = - 3{x^2} + x + 1$ có 2 nghiệm phân biệt $x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}$

Hệ số $a = - 3 < 0$

Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy $f\left( x \right) > 0$$ \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}$

Vậy tập nghiệm của bất phương trình là $\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)$

c) $4{x^2} + 4x + 1 \ge 0$

Tam thức bậc hai $f\left( x \right) = 4{x^2} + 4x + 1$ có nghiệm duy nhất $x = \frac{{ - 1}}{2}$

hệ số $a = 4 > 0$

Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy $f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}$

Vậy tập nghiệm của bất phương trình là $\mathbb{R}$

d) $ - 16{x^2} + 8x - 1 < 0$

Tam thức bậc hai $f\left( x \right) = - 16{x^2} + 8x - 1$ có nghiệm duy nhất $x = \frac{1}{4}$

hệ số $a = - 16 < 0$

Ta có bảng xét dấu f(x) như sau:

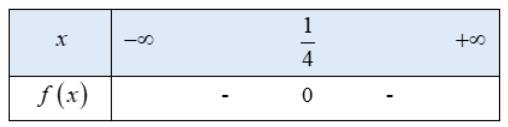
Từ bảng xét dấu ta thấy $f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}$

Vậy tập nghiệm của bất phương trình là $\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}$

e) $2{x^2} + x + 3 < 0$

Ta có $\Delta = {1^2} - 4.2.3 = - 23 < 0$ và có $a = 2 > 0$

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho $2{x^2} + x + 3$ mang dấu “-” là $\emptyset $

Vậy tập nghiệm của bất phương trình $2{x^2} + x + 3 < 0$ là $\emptyset $

g) $ - 3{x^2} + 4x - 5 < 0$

Tam thức bậc hai $f\left( x \right) = - 3{x^2} + 4x - 5$ có $\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0$ và có $a = - 3 < 0$

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho $ - 3{x^2} + 4x - 5$ mang dấu “-” là $\mathbb{R}$

Vậy tập nghiệm của bất phương trình $ - 3{x^2} + 4x - 5 < 0$ là $\mathbb{R}$

Đúng(0)

PT

Pham Trong Bach

4 tháng 1 2017

Giải các bất phương trình g ' ( x ) ≤ 0 v ớ i g ( x ) = x 2 - 5 x + 4 x - 2

#Toán lớp 11

1

CM

Cao Minh Tâm

4 tháng 1 2017

Vô nghiệm.

Đúng(0)

TB

Tạ Bảo

4 tháng 3 2022

1.Giải các phương trình sau : a,7x+35=0 b, 8-x/x-7 -8 =1/x-7 2.giải bất phương trình sau : 18-3x(1-x)_< 3x^2-3x

#Toán lớp 8

3

NL

Nguyễn Lê Phước Thịnh

4 tháng 3 2022

a: 7x+35=0

=>7x=-35

=>x=-5

b: $\dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}$

=>8-x-8(x-7)=1

=>8-x-8x+56=1

=>-9x+64=1

=>-9x=-63

hay x=7(loại)

Đúng(1)

NH

Nguyễn Huy Tú

4 tháng 3 2022

a, $7x=-35\Leftrightarrow x=-5$

b, đk : x khác 7

$8-x-8x+56=1\Leftrightarrow-9x=-63\Leftrightarrow x=7\left(ktm\right)$

vậy pt vô nghiệm

2, thiếu đề

Đúng(0)

HB

Hạ Băng Băng

4 tháng 3 2021

Câu 1:Tìm nghiệm của bất phương trình x²-5x-6-6|x+1|≤0 Câu 2: Giải bất phương trình|x²-3|+2x≥0

#Toán lớp 10

0

BW

BoSo WF

12 tháng 4 2022

1) Giải các phương trình sau : a) x-3/x=2-x-3/x+3 b) 3x^2-2x-16=0 2) Giải bất phương trình sau: 4x-3/4>3x-5/3-2x-7/12

#Toán lớp 8

2

Y

YangSu

12 tháng 4 2022

$a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}$$\left(đk:x\ne0,-3\right)$

$\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0$

$\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0$

$\Leftrightarrow x^2-9-x^2+3x=0$

$\Leftrightarrow3x-9=0$

$\Leftrightarrow3x=9$

$\Leftrightarrow x=3\left(n\right)$

Vậy $S=\left\{3\right\}$

Đúng(1)

Y

YangSu

12 tháng 4 2022

$b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}$

$\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0$

$\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0$

$\Leftrightarrow12x-9-12x+20+2x-7>0$

$\Leftrightarrow2x+4>0$

$\Leftrightarrow2x>-4$

$\Leftrightarrow x>-2$

Đúng(1)

QT

Quoc Tran Anh Le

Giáo viên

23 tháng 9 2023

Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc hai một ẩn? Vì sao?
a) $-2 x+2<0$
b) $\frac{1}{2} y^2-\sqrt{2}(y+1) \leq 0$
c) $y^2+x^2-2 x \geq 0$

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

23 tháng 9 2023

a) $ - 2x + 2 < 0$ không là bất phương trình bậc hai một ẩn vì bậc của bất phương trình này là bậc 1.

b) $\frac{1}{2}{y^2} - \sqrt 2 \left( {y + 1} \right) \le 0$ là bất phương trình bậc hai một ẩn vì bậc của bất phương trình này là bậc 2 và có đúng 1 ẩn là y.

c) ${y^2} + {x^2} - 2x \ge 0$ không là bất phương trình bậc hai một ẩn vì có 2 ẩn là x và y.

Đúng(0)

HT

Hồ thị lbind

31 tháng 3 2020

I.ĐẠI SỐ CHƯƠNG 4. BẤT ĐẲNG THỨC. BẤT PHƯƠNG TRÌNH 1. Bất phương trình Khái niệm bất phương trình. Nghiệm của bất phương trình. Bất phương trình tương đương. Phép biến đổi tương đương các bất phương trình. 2. Dấu của một nhị thức bậc nhất Dấu của một nhị thức bậc nhất. Hệ bất phương trình bậc nhất một ẩn. 3. Dấu của tam thức bậc hai Dấu của tam thức bậc...

Đọc tiếp

#Toán lớp 10

0

BL

Bích Lê

16 tháng 4 2022

Giải phương trình và bất phương trình

a) $3\sqrt{-x^2+x+6}+2\left(2x-1\right)>0$

b)$\sqrt{2x^2+8x+5}+\sqrt{2x^2-4x+5}=6\sqrt{x}$

#Toán lớp 10

3

NV

Nguyễn Việt Lâm

Giáo viên

16 tháng 4 2022

a.

$3\sqrt{-x^2+x+6}\ge2\left(1-2x\right)$

$\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-x^2+x+6\ge0\\1-2x< 0\end{matrix}\right.\\\left\{{}\begin{matrix}1-2x\ge0\\9\left(-x^2+x+6\right)\ge4\left(1-2x\right)^2\end{matrix}\right.\end{matrix}\right.$

$\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-2\le x\le3\\x>\dfrac{1}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\25\left(x^2-x-2\right)\le0\end{matrix}\right.\end{matrix}\right.$

$\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}< x\le3\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\-1\le x\le2\end{matrix}\right.\end{matrix}\right.$

$\Rightarrow-1\le x\le3$

Đúng(0)

NV

Nguyễn Việt Lâm

Giáo viên

16 tháng 4 2022

b.

ĐKXĐ: $x\ge0$

$\Leftrightarrow\sqrt{2x^2+8x+5}-4\sqrt{x}+\sqrt{2x^2-4x+5}-2\sqrt{x}=0$

$\Leftrightarrow\dfrac{2x^2+8x+5-16x}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-4x+5-4x}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0$

$\Leftrightarrow\dfrac{2x^2-8x+5}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-8x+5}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0$

$\Leftrightarrow\left(2x^2-8x+5\right)\left(\dfrac{1}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{1}{\sqrt{2x^2-4x+5}+2\sqrt{x}}\right)=0$

$\Leftrightarrow2x^2-8x+5=0$

$\Leftrightarrow x=\dfrac{4\pm\sqrt{6}}{2}$

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP