Biết
a
b
(trong đó
a
b
là phân số tối giản và
a
,
b
∈
ℕ
*
)
là giá trị của tham số thực m để cho hàm số
y
=
2
3
x
3
−
m
x
2
−
2
3
m
2
−
1
x
+
2
3
có hai điểm cực trị
x
1
,
x
2
sao cho
x
1
x
2
+
2
...
Đọc tiếp
Biết a b (trong đó a b là phân số tối giản và a , b ∈ ℕ * ) là giá trị của tham số thực m để cho hàm số y = 2 3 x 3 − m x 2 − 2 3 m 2 − 1 x + 2 3 có hai điểm cực trị x 1 , x 2 sao cho x 1 x 2 + 2 x 1 + x 2 = 1. Tính giá trị biểu thức S = a 2 + b 2 .
A. S = 13
B. S = 25
C. S = 10
D. S = 34
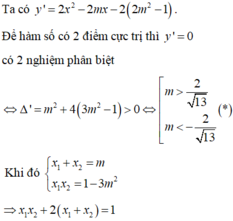
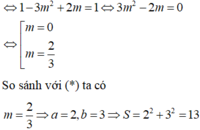
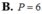
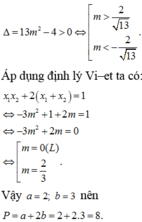
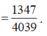
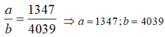
Đáp án A.
Ta có y ' = 2 x 2 − 2 m x − 6 m 2 + 2.
Để hàm số có 2 điểm cực trị
⇔ y ' = 0 có 2 nghiệm phân biệt.
⇔ Δ ' = m 2 + 4 3 m 2 − 1 > 0 ⇔ 13 m 2 − 4 > 0 ⇔ m > 2 13 m < − 2 13 .
Khi đó, theo Viet ta có
x 1 + x 2 = m x 1 x 2 = 1 − 3 m 2 .
Mà x 1 x 2 + 2 x 1 + x 2 = 1 nên suy ra
1 − 3 m 2 + 2 m = 1 ⇔ 3 m 2 − 2 m ⇔ m = 0 m = 2 3 .
Kết hợp với điều kiện, ta được
m = 2 3 = a b ⇒ a = 2 b = 3 → S = 2 2 + 3 2 = 13.