Cho hàm số y = f(x) có đạo hàm tại x = 1. Gọi d 1 , d 2 lần lượt là tiếp tuyến của đồ thị hàm số y = f x và y = g x = x . f 2 x − 1 tại điểm có hoành độ x = 1. Biết rằng hai đường thẳng d 1 , d 2 vuông góc nhau. Khẳng định nào sau đây đúng?
A. 2 < f 1 < 2.
B. f 1 ≤ 2 .
C. f 1 ≥ 2 2 .
D. 2 ≤ f 1 < 2 2 .


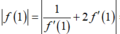
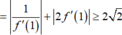
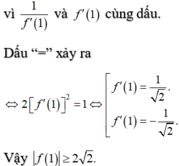
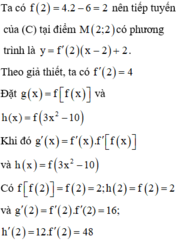





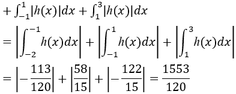




Đáp án C.
Ta có:
g x = x . f 2 x − 1 ⇒ g ' x = f 2 x − 1 + 2 x . f ' 2 x − 1
Suy ra g ' 1 = f 1 + 2 f ' 1 mà d 1 vuông góc với d 2 ⇒ f ' 1 . g ' 1 = − 1
⇔ f ' 1 . f 1 + 2 f ' 1 = − 1 ⇔ 2. f ' 1 2 + f 1 + 1 = 0 ( * )
Phương trình (*) có nghiệm khi và chỉ khi:
Δ = f 1 2 − 4.2 ≥ 0 ⇔ f 1 ≥ 2 2 .