Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): mx + 2y - z + 1 = 0 (m là tam số). Mặt phẳng (P) cắt mặt cầu (S): x - 2 2 + y - 1 2 + z 2 = 9 theo một đường tròn có bán kính bằng 2. Tìm tất cả các giá trị thực của tham số m.
A. m = ± 1
B. m = ± 2 + 5
C. m = 6 ± 2 5
D. m = ± 4



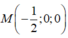


Đáp án C.
Mặt cầu (S) có tâm I(2;1;0) bán kính R = 3. Ta có d I ; P = 3 2 - 2 2 = 5
Do đó 2 m + 3 m 2 + 5 = 5 ⇔ 2 m + 3 2 = 5 m 2 + 25 ⇔ m = 6 ± 2 5 .