Trong 1 hội trường có một số băng ghế, mỗi băng ghế quy định số người ngồi như nhau. Nếu bớt 2 băng ghế, mỗi băng ghế thêm 1 người thì thêm được 8 người. Nếu thêm 3 băng ghế, mỗi băng ghế bớt đi 1 người thì giảm 8 người. Hỏi trong hội trường có bao nhêu băng ghế?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Gọi số ghế băng của hội trường là x ( ghế , \(x\in N\) * )
- Gọi số người đến hội trường là y ( người , \(y\in N\)* )
-> Số người dự định ngồi trên 1 ghế là : \(\frac{y}{x}\) ( người )
Theo đề bài nếu bớt 2 ghế băng và mỗi ghế băng thêm 1 người thì thêm được 8 chỗ \(\left(x-2\right)\left(\frac{y}{x}+1\right)-8=y\left(I\right)\)
Theo đề bài nếu thêm 3 ghế băng và mỗi ghế băng ngồi rút đi 1 người thì giảm 8 chỗ \(\left(x+3\right)\left(\frac{y}{x}-1\right)+8=y\left(II\right)\)
- Từ ( I ) và ( II ) ta có hệ phương trình : \(\left\{{}\begin{matrix}\left(x-2\right)\left(\frac{y}{x}+1\right)-8=y\\\left(x+3\right)\left(\frac{y}{x}-1\right)+8=y\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y-\frac{2y}{x}+a-2-8-y=0\\y+\frac{3y}{x}-x-3+8-y=0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}-\frac{2y}{x}+x=10\\\frac{3y}{x}-x=-5\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}-\frac{2y}{x}+\frac{x^2}{x}=\frac{10x}{x}\\\frac{3y}{x}-\frac{x^2}{x}=-\frac{5x}{x}\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x^2-2y=10x\\x^2-3y=5x\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x^2-2\left(5x\right)=10x\\y=5x\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x^2-20x=0\\y=5x\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x\left(x-20\right)=0\\y=5x\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\left(KTM\right)\\x=20\left(TM\right)\end{matrix}\right.\\y=5.20=100\end{matrix}\right.\)
Vậy số băng ghế trong hội trường là 20 băng ghế .

Gọi số ghế băng lúc đầu là x ( ghế băng), ( x∈N*, x> 2)
Số học sinh ngồi trên mỗi ghế là 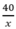 ( học sinh ) .
( học sinh ) .
Khi bớt đi 2 ghế băng thì còn lại x- 2 ( ghế băng ) và khi đó, mỗi ghế có 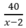 học sinh ngồi.
học sinh ngồi.
Theo giả thiết, nếu ta bớt đi 2 ghế băng thì mỗi ghế còn lại phải xếp thêm 1 học sinh nên ta có phương trình:
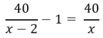
⇔ 40 x − x ( x − 2 ) = 40 ( x − 2 ) ⇔ 40 x − x 2 + 2 x = 40 x − 80 ⇔ − x 2 + 2 x + 80 = 0
Có a = -1, b= 2; c = 80 và ∆ = 2 2 – 4 . ( - 1 ) . 80 = 324
Nên phương trình trên có 2 nghiệm là: x1 = -8 ( loại) và x2 =10 ( thỏa mãn)
Vậy lúc đầu có 10 ghế băng.

Gọi số ghế băng lúc đầu là x ( ghế băng), ( x∈N*, x> 2)
Số học sinh ngồi trên mỗi ghế là 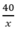 ( học sinh ) .
( học sinh ) .
Khi bớt đi 2 ghế băng thì còn lại x- 2 ( ghế băng ) và khi đó, mỗi ghế có 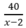 học sinh ngồi.
học sinh ngồi.
Theo giả thiết, nếu ta bớt đi 2 ghế băng thì mỗi ghế còn lại phải xếp thêm 1 học sinh nên ta có phương trình:

⇔ 40 x − x ( x − 2 ) = 40 ( x − 2 ) ⇔ 40 x − x 2 + 2 x = 40 x − 80 ⇔ − x 2 + 2 x + 80 = 0
Có a = -1, b= 2; c = 80 và ∆ = 2 2 – 4 . ( - 1 ) . 80 = 324
Nên phương trình trên có 2 nghiệm là: x1 = -8 ( loại) và x2 =10 ( thỏa mãn)
Vậy lúc đầu có 10 ghế băng.

Phan Minh Anh
Gọi x là số ghế băng ban đầu (x thuôc N*)
Suy ra số học sinh ở mỗi ghế băng là 40:x
Nếu bớt đi 2 ghế băng (x-2) thì mỗi ghế còn lại phải xếp thêm 1 hs (x+1)
Hay (x-2).(x+1) =40
<=> x2 -2x -80 =0
<=> x=10
Vậy số ghế băng ban đầu là 10 ghế

Gọi số dãy ghế là x>2 và số người một dãy ghế là y>1
\(\Rightarrow\) Số người dự định: \(xy\)
Khi bớt 2 dãy ghế và mỗi ghế thêm 1 người thì số người ngồi: \(\left(x-2\right)\left(y+1\right)\)
Khi thêm 3 dãy ghế và mỗi dãy ghế bớt 1 người thì số người: \(\left(x+3\right)\left(y-1\right)\)
Theo bài ra ta có hệ: \(\left\{{}\begin{matrix}\left(x-2\right)\left(y+1\right)=xy+8\\\left(x+3\right)\left(y-1\right)=xy-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2y=10\\-x+3y=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=20\\y=5\end{matrix}\right.\)
Vậy có 20 dãy ghế

Gọi số dãy ghế ban đầu của hội trường là a (dãy), số chỗ ở mỗi dãy ban đầu ở hội trường là b (chỗ)
Nếu bớt 2 dãy ghế và mỗi dãy thêm 1 chỗ thì thêm được 8 chỗ: \(\left(a-2\right)\left(b+1\right)=ab+8\Leftrightarrow ab+a-2b-2=ab+8\Leftrightarrow a-2b-10=0\left(1\right)\)
Nếu thêm 3 dãy ghế và mỗi dãy ghế bớt đi 1 chỗ thì giảm 8 chỗ:
\(\left(a+3\right)\left(b-1\right)=ab-8\Leftrightarrow ab-a+3b-3=ab-8\Leftrightarrow-a+3b+5=0\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình: \(\left\{{}\begin{matrix}a-2b=10\\-a+3b=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=20\\b=5\end{matrix}\right.\)
Vậy số dãy ghế ban đầu của hội trường là 20 dãy
