Em sẽ nói thế nào để giúp cậu bé chọn được hai chiếc giày cùng đôi ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 8 2020
1, bước đi tập tễnh
2,cậu bé nghĩ do đường khấp khểnh
3, hai chiếc giày ở nhà vẫn chiếc thấp chiếc cao
20 tháng 8 2020
1. Vì cậu bé xỏ nhầm giầy nên cậu bước tập tễnh
2. Khi thấy khó khăn cậu bé nghĩ : Sao hôm nay mình một chân ngắn một chân dài ? Hay tại đường khấp khểnh ?
3.Cậu bé thấy 2 chiếc ở nhà vẫn chiếc thấp chiếc cao
DH
1
13 tháng 6 2018
Cậu bé thấy hai chiếc giày ở nhà vẫn chiếc thấp, chiếc cao.
21 tháng 1 2016
Chọn ra 3 chiếc. Kiểu gì cũng ra ít nhất 1 dôi giày cùng màu.
CM
27 tháng 3 2019
Không gian mẫu là kết quả của việc chọn ngẫu nhiên 2 chiếc giày trong số 8 chiếc giày.
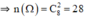
A: “ Chọn được 2 chiếc tạo thành một đôi”
⇒ n(A) = 4 (Vì có 4 đôi).
VT
Vũ Thị Minh Ánh
Giáo viên
14 tháng 12 2022
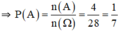
\(n\left(\Omega\right)=C^4_{10}=210\)
A: "Không chọn được hai chiếc nào tạo thành một đôi".
\(\overline{A}\): "Chọn được ít nhất hai chiếc tạo thành một đôi".
\(n\left(\overline{A}\right)=C^1_5\cdot C_8^2=140\).
\(n\left(A\right)=210-140=70\).
\(P\left(A\right)=\dfrac{70}{210}=\dfrac{1}{3}\).
CM
18 tháng 5 2019
Ba đôi giày có số chiếc giày là :
3x 2 = 6 (chiếc)
Nếu lấy ra 3 chiếc giày thì trường hợp xấu nhất là 3 chiếc thuộc ba đôi khác nhau.
Vậy lấy thêm chiếc thứ tư thì chắc chắn nó sẽ là chiếc giày còn lại của một trong ba đôi. Do đó lấy 4 chiếc giày bất kì chắc chắn sẽ có hai chiêc giày cùng một đôi.
MH
9 tháng 4 2017
Phép thử T được xét là: "Lấy ngẫu nhiên 2 chiếc giày từ 4 đôi giày có cỡ khác nhau".
Mỗi một kết quả có thể là một tổ hợp chập 2 của 8 chiếc giày. Do đó số các kết quả có thể có thể có của phép thử T là n(Ω) = C28 = = 28.
Vì lấy ngẫu nhiên, nên các kết quả có thể có của phép thử T là đồng khả năng. Gọi A là biến cố: "Lấy được hai chiếc giày tạo thành một đôi". Mỗi một kết quả có thể có thuận lợi cho A là một đôi giày trong 4 đôi giày đã cho. Do đó số các kết quả có thể có thuận lợi cho A là n(A) = 4. Suy ra P(A) = =
.
Để giúp cậu bé chọn được hai chiếc giày cùng đôi, em sẽ nói :
- Bạn hãy đặt 4 chiếc giày trước mặt và hãy chọn ra 2 chiếc giống nhau để đi.