Viết số thập phân vô hạn tuần hoàn 2,131131131… (chu kì 131) dưới dạng phân số.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
1
,...,131/
NM
Nguyễn Minh Quang
Giáo viên
1 tháng 11 2021
Phân số hữu hạn là : \(\frac{5}{8}=0.625,-\frac{3}{20}=-0.15\)\(\frac{14}{35}=\frac{2}{5}=0.4\) vì mẫu tối giản của chúng là tích của các lũy thừa 2 và 5.
Phân số còn lại là vô hạn tuần hoàn vì mẫu của chúng không phân tích được thành tích của các lúy thừa 2 và 5.
Số \(\frac{4}{11}=0.\left(36\right),\frac{15}{22}=0.68\left(18\right),-\frac{7}{12}=-0.58\left(3\right)\)
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Ta có: \(\frac{1}{4} = 0,25\). Đây là số thập phân hữu hạn.
\( - \frac{2}{{11}} = - 0,1818....\). Đây là số thập phân vô hạn tuần hoàn. Chu kì của nó là 18. Ta viết \( - \frac{2}{{11}}=-0,(18)\)
CM
24 tháng 3 2017
Ta có: a= 1,02020202... ( chu kì 2)
= 1 + 0,02+ 0,0002+ 0,000002 + .....
Là tổng của cấp số nhân lùi vô hạn có số hạng đầu là
PT
1
LN
14 tháng 10 2017
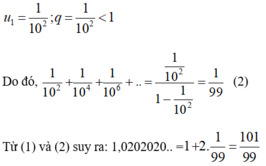
a) Các phân số được viết dưới dạng tối giản là:
\(\dfrac{5}{8};\dfrac{-3}{20};\dfrac{4}{11};\dfrac{15}{22};\dfrac{-7}{12};\dfrac{2}{5}\)
Lần lượt xét các mẫu:
8 = 23; 20 = 22.5 11
22 = 2.11 12 = 22.3 35 = 7.5
+ Các mẫu không chứa thừa số nguyên tố nào khác 2 và 5 là 8; 20; 5 nên các phân số viết dưới dạng số thập phân hữu hạn.
Kết quả là:
\(\dfrac{5}{8}=0,625\) \(\dfrac{-3}{20}=-0,15\) \(\dfrac{14}{35}=\dfrac{2}{5}=0,4\)
+ Các mẫu có chứa thừa số nguyên tố khác 2 và 5 là 11, 22, 12 nên các phân số viết dưới dạng số thập phân vô hạn tuần hoàn.
Kết quả là:
\(\dfrac{4}{11}=0,\left(36\right)\) \(\dfrac{-3}{20}=0,6\left(81\right)\) \(\dfrac{-7}{12}=-0,58\left(3\right)\)
b) Các phân số được viết dạng số thập phân hữu hạn
\(\dfrac{5}{8}=0,625\) \(\dfrac{-3}{20}=0,15\) \(\dfrac{14}{35}=0,4\)
Các số thập phân vô hạn tuần hoàn là:
\(\dfrac{15}{22}=0,6\left(81\right)\) \(\dfrac{-7}{12}=-0,58\left(3\right)\) \(\dfrac{4}{11}=0,\left(36\right)\)
18 tháng 4 2017
a) Các phân số được viết dưới dạng tối giản là:
58;−320;411;1522;−712;2558;−320;411;1522;−712;25.
Lần lượt xét các mẫu:
8 = 23; 20 = 22.5 11
22 = 2.11 12 = 22.3 35 = 7.5
+ Các mẫu không chứa thừa số nguyên tố nào khác 2 và 5 là 8; 20; 5 nên các phân số viết dưới dạng số thập phân hữu hạn.
Kết quả là:
58=0,625;58=0,625; −320=−0,15−320=−0,15; 1435=25=0,41435=25=0,4
+ Các mẫu có chứa thừa số nguyên tố khác 2 và 5 là 11, 22, 12 nên các phân số viết dưới dạng số thập phân vô hạn tuần hoàn.
Kết quả là:
411=0,(36)411=0,(36) 1522=0,6(81)1522=0,6(81) −712=0,58(3)−712=0,58(3)
b) Các phân số được viết dạng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn là:
58=0,62558=0,625 −320=−0,15−320=−0,15 411=0,(36)411=0,(36)
1522=0,6(81)1522=0,6(81) −712=0,58(3)−712=0,58(3) 1435=0,4
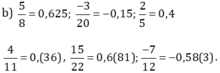
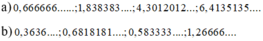
2,131131131...
(Vì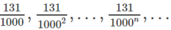
là một cấp số nhân lùi vô hạn với công bội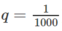
)