Trên đồ thị (C) của hàm số y = 3 - x x - 1 có bao nhiêu điểm có tọa độ nguyên ?
A. 2
B. 1
C. 3.
D. 4.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
16 tháng 4 2019
Đáp án A
Gọi 
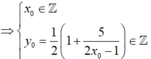
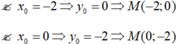
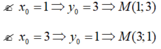
Vậy trên đồ thị (C) có bốn điểm có tọa độ là các số nguyên.
PT
1
CM
26 tháng 1 2019
Đáp án D
Gọi 
.
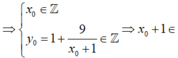
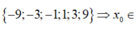
Vậy trên đồ thị (C) có sáu điểm có tọa độ là các số nguyên.
13 tháng 11 2021
b: Toạ độ giao điểm của (d) và (d1) là:
\(\left\{{}\begin{matrix}\dfrac{1}{2}x+5=-\dfrac{3}{2}x+1\\y=\dfrac{1}{2}x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-4\\y=\dfrac{1}{2}x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=\dfrac{1}{2}\cdot\left(-2\right)+5=5-1=4\end{matrix}\right.\)
L
15 tháng 1 2020
\(a)\)Vì đths \(y=\left(2m-\frac{1}{2}\right)x\)đi qua \(A\left(-2;5\right)\)
\(\Rightarrow\)Thay \(x=-2;y=5\)vào hàm số
\(\Leftrightarrow\left(2m-\frac{1}{2}\right)\left(-2\right)=5\)
\(\Leftrightarrow2m-\frac{1}{2}=-\frac{5}{2}\)
\(\Leftrightarrow2m=-2\)
\(\Leftrightarrow m=-1\)
\(b)m=-1\)
\(\Leftrightarrow y=-\frac{5}{2}x\)
\(c)\)Lập bảng giá trị:
| \(x\) | \(0\) | \(-2\) |
| \(y=-\frac{5}{2}x\) | \(0\) | \(5\) |
\(\Rightarrow\)Đths \(y=-\frac{5}{2}x\)là một đường thẳng đi qua hai điểm \(O\left(0;0\right);\left(-2;5\right)\)
Tự vẽ :<
\(d)\)Chỉ cần thành hoành độ hoặc tung độ là x hoặc y vào đths trên là tìm được cái còn lại. Khi đó tìm được tọa độ của 2 diểm trên.
KV
6 tháng 12 2023
a) Đồ thị:
b) Gọi giao điểm của đồ thị của hàm số y = x - 1 với trục tung, với trục hoành lần lượt là 2 điểm B và C
Thay x = 0 vào hàm số y = x - 1 ta có:
y = 0 - 1 = - 1
⇒ B(0; -1)
Thay y = 0 vào hàm số y = x - 1 ta có:
x - 1 = 0
⇔ x = 1
⇒ C(1; 0)
c) Gọi (t): y = ax + b (a 0)
Do (t) // (d) nên a = -2
⇒ (t): y = -2x + b
Thay y = -3 vào (d') ta có:
x - 1 = -3
⇔ x = -3 + 1
⇔ x = -2
Thay x = -2; y = -3 vào (t) ta có:
-2.(-2) + b = -3
⇔ 4 + b = -3
⇔ b = -3 - 4
⇔ b = -7
Vậy (t): y = -2x - 7
PT
1
CM
25 tháng 8 2017
Đáp án B
Gọi 
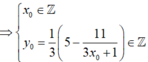
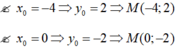
Vậy trên đồ thị (C) có hai điểm có tọa độ là các số nguyên.
Đáp án D
Ta có .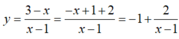
Vậy có 4 điểm thỏa yêu cầu bài toán