Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Gọi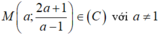 
với
a
≢
1
.
Tiệm cận đừng và tiệm cận ngang của (C) lần lượt có phương trình
.
Khoảng cách từ M đến tiệm cận đứng là
Khoảng cách từ M đến tiệm cận ngang là
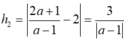
Tổng khoảng cách từ M đến hai đường tiệm cận bằng 4 nên ta có:
.
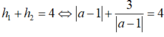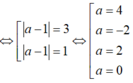
Vậy các điểm cần tìm là: 
.
Đáp án B
Gọi M a; a + 2 a − 2 thuộc đồ thị hàm số
d ( M;TCD ) = a − 2
d ( M;TCN ) = 4 a − 2
Tổng khoảng cách= a − 2 + 4 a − 2 ≥ 2 a − 2 . 4 a − 2 = 4
Dấu bằng xảy ra khi a − 2 = 4 a − 2 ⇔ a=4 a=0 do hoành độ dương nên a=4
Vậy M(4;3)
Đáp án B
Gọi M a; a + 2 a − 2 thuộc đồ thị hàm số
d ( M;TCD ) = a − 2
d ( M;TCN ) = 4 a − 2
Tổng khoảng cách = a − 2 + 4 a − 2 ≥ 2 a − 2 . 4 a − 2 = 4
Dấu bằng xảy ra khi a − 2 = 4 a − 2 ⇔ a=4 a=0 do hoành độ dương nên a=4
Vậy M(4;3)
+ Đồ thị hàm số đã cho có tiệm cận đứng là x= -2 và tiệm cận ngang là y= 1.
Giao điểm hai đường tiệm cận là I ( -2; 1) .
Ta có:
A ( a ; 1 - 3 a + 2 ) ∈ ( C ) , B ( b ; 1 - 3 b + 2 ) ∈ ( C ) . I A → = ( a + 2 ; - 3 a + 2 ) , I B → = ( b + 2 ; - 3 b + 2 ) .
Đặt a1== a+ 2 ; b1= b+ 2( a1≠ 0 ; b1≠0 ; a1 ≠ b1
Tam giác ABI đều khi và chỉ khi
Ta có (1)
+ Trường hợp a1= b1 loại
+ Trường hợp a1= - b1 ; a1b1 = -3 (loại vì không thỏa (2) .
+ Trường hợp a1 b1 =3 thay vào ( 2) ta được
3 + 9 3 a 1 2 + 9 a 1 2 = 1 2 ⇔ a 1 2 + 9 a 1 2 = 12 .
Vậy AB=IA= a 1 2 + 9 a 1 2 = 2 3 .
Chọn B.
Đáp án B