Cho hình chóp S.ABCD, có đáy là hình vuông cạnh a, SCD là tam giác đều và (SCD) vuông góc với đáy. Tính khoảng cách h từ A đến mặt phẳng (SBD).
A. h = 3 7 a
B. h = 2 3 7 a
C. h = 21 7 a
D. h = 42 7 a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi H là trung điểm của AD, vì ΔASD cân ở S nên SH ⊥ AD.
Vì (SAD)⊥(ABCD) nên SH ⊥ (ABCD). Kẻ HI ⊥ SD.
Vì DC ⊥ AD, DC ⊥ SH nên DC ⊥ (SAD). Do đó DC ⊥ HI.
Kết hợp với HI ⊥ SD, suy ra HI ⊥ (SDC).
Vì AB // (SDC) nên d(B; (SDC)) = d(A; (SDC)) = 2HI
Ta có
Ta lại có


Đáp án A
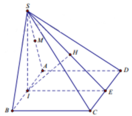
Gọi I, E lần lượt là trung điểm của AB và CD
Vì S M S A = 1 2 ⇒ d M ; S C D = 1 2 d A ; S C A = 1 2 d I ; S C A
= 1 2 I H , trong đó H là hình chiếu của I lên SE
Ta có 1 I H 2 = 1 I S 2 + 1 I E 2 = 1 a 2 − a 2 2 + 1 a 2 = 7 3 a 2
⇒ I H = a 21 7 ⇒ d M ; S C D = 1 2 . a 21 7 = a 21 14

1) Gọi H là trung điểm của AB.
ΔSAB đều → SH ⊥ AB
mà (SAB) ⊥ (ABCD) → SH⊥ (ABCD)
Vậy H là chân đường cao của khối chóp.
2) Ta có tam giác SAB đều nên SA =a3√2
suy ra V=13SABCD.SH=a33√6

Đáp án C
Theo dữ kiện đề bài cho, dễ dàng chứng minh được ΔACD vuông tại cân C và A C = A D 2 = a 2 .
C D ⊥ A C C D ⊥ S A ⇒ C D ⊥ S A C ⇒ S A C ⊥ S C D
Mà S A C ∩ S C D = S C , từ A kẻ A H ⊥ S C . Khi đó d A ; S C D = A H .
Tam giác SAC vuông tại
A: 1 A H 2 = 1 S A 2 + 1 A C 2 = 1 a 2 + 1 2 a 2 = 3 2 a 2 ⇒ d A ; S C D = A H = a 2 3
Mặt khác: A D ∩ S C D = D và M là trung điểm AD nên:
d M ; S C D d A ; S C D = M D A D = 1 2 ⇒ d M ; S C D = 1 2 d A ; S C D = a 6 6
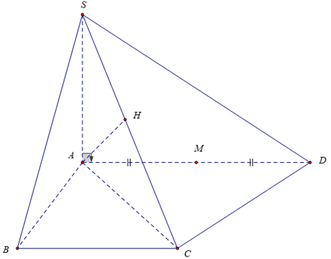

Do SAB là tam giác đều \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}\left(SAB\right)\perp\left(ABCD\right)\\AB=\left(SAB\right)\cap\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Gọi E là trung điểm CD, từ H kẻ \(HF\perp SE\) (F thuộc SE)
\(\left\{{}\begin{matrix}HE\perp CD\\SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SHE\right)\)
\(\Rightarrow CD\perp HF\)
\(\Rightarrow HF\perp\left(SCD\right)\Rightarrow HF=d\left(H;\left(SCD\right)\right)\)
\(HE=BC=a\) ; \(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
Hệ thức lượng:
\(HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{21}}{7}\)
Đáp án C
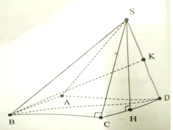
Gọi H là trung điểm của CD, dễ thấy SH là đường cao của hình chóp.
Suy ra
Để ý rằng SB 2 = SH 2 + BH 2 = SH 2 + BC 2 + CH 2 = 3 a 2 / 4 + a 2 + a 2 / 4 = 2 a 2 .
Suy ra BS = BD = a 2 , gọi K là trung điểm của SD ta có: