Ba quả cầu được đặt vào ba cái hộp khác nhau (không nhất thiết hộp nào cũng có quả cầu). Hỏi có bao nhiêu cách đặt,nếu:
a) Các quả cầu giống hệt nhau (không phân biệt)?
b) Các quả cầu đôi một khác nhau?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 5 2017
a) Trong trường hợp này, số cách đặt bằng số các nghiệm \(\left(x_1,x_2,x_3\right)\) nguyên, không âm của phương trình \(x_1+x_2+x_3=3\). Từ đó, đáp số cần tìm là \(C^2_5=10\)
b) Quả thứ nhất có 3 cách đặt
Quả thứ hai có 3 cách đặt
Quả thứ ba có 3 cách đặt
Vậy số cách đặt là \(3^3=27\)
CM
23 tháng 12 2019
Chọn A
* Không gian mẫu là n ( Ω ) = 6
* Gọi biến cố A: " Các quả cầu cùng màu thì vào chung một hộp”
Bỏ 3 quả cầu vào một hộp, bỏ 3 quả màu xanh vào hộp còn lại có 2 cách
=> n(A) = 2
* Xác suất của biến cố A là
CM
1 tháng 4 2019
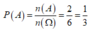
Chọn C.
Phương pháp:
Sử dụng kiến thức về tổ hợp và hai qui tắc đếm cơ bản.
Chia các trường hợp có thể xảy ra để tìm kết quả.
Cách giải:
Lấy ngẫu nhiên 5 quả cầu mà số quả cầu xanh lớn hơn số quả cầu đỏ ta có các trường hợp sau :
TH1: 5 quả cầu xanh, 0 quả cầu đỏ thì số cách chọn là C 5 5 (cách)
TH2 : 4 quả cầu xanh, 1 quả cầu đỏ thì số cách chọn là C 5 4 . C 7 1 (cách)
TH3 : 3 quả cầu xanh, 2 quả cầu đỏ thì số cách chọn là C 5 3 . C 7 2 (cách)
Vậy số cách chọn thỏa mãn đề bài là C 5 5 + C 5 4 . C 7 1 + C 5 3 . C 7 2 =246 (cách)
a) Trong trường hợp này, số cách đặt bằng số các nghiệm ( x 1 , x 2 , x 3 ) nguyên, không âm của phương trình x 1 + x 2 + x 3 = 3 . Từ đó, đáp số cần tìm là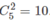
b) Quả thứ nhất có 3 cách đặt;
Quả thứ hai có 3 cách đặt;
Quả thứ ba có 3 cách đặt.
Vậy số cách đặt là 3 3 = 27 .