Lập phương trình mặt phẳng: Chứa trục Ox và điểm P(4; -1; 2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 12 2017
Đáp án B
Từ giả thiết suy ra
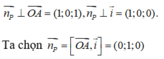
Từ đó suy ra phương trình của mặt phẳng (P) là: 1(y - 0) = 0 ⇔ y = 0
PT
1
PT
1
CM
16 tháng 1 2017
(Q) chứa trục Oy và điểm Q(1; 4; -3)
+ (Q) chứa Oy ⇒ nhận j → = (0; 1; 0) là 1 vtcp).
+ (Q) chứa O(0 ; 0 ; 0) và Q(1 ; 4 ; -3) ⇒ nhận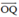 
= ( 1 ; 4 ; -3) là 1 vtcp
⇒ (Q) nhận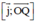 
= (-3; 0; -1) là 1 vtpt
⇒ (Q): -3(x – 0) – 1.(z – 0) = 0
hay (Q): 3x + z = 0.
PT
1
CM
12 tháng 8 2019
(R) chứa trục Oz và điểm R(3; -4; 7)
+ (R) chứa Oz ⇒ nhận k → = (0; 0; 1) là 1 vtcp.
+ (R) chứa O(0 ; 0 ; 0) và R(3 ; -4 ; 7) ⇒ nhận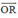 
= ( 3 ; -4 ; 7) là 1 vtcp
⇒ (R) nhận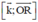 
= (4; 3; 0) là 1 vtpt
⇒ (R): 4(x – 0) + 3.(y – 0) = 0
hay (R): 4x + 3y = 0.
KH
1 tháng 4 2017
Giải:
a) Gọi (α) là mặt phẳng qua P và chứa trục Ox, thì (α) qua điểm O(0 ; 0 ; 0) và chứa giá của các vectơ (4 ; -1 ; 2) và
( 1 ; 0 ;0). Khi đó
=(0 ; 2 ; 1) là vectơ pháp tuyến của (α).
Phương trình mặt phẳng (α) có dạng: 2y + z = 0.
b) Tương tự phần a) mặt phẳng (β) qua điểm Q(1 ; 4 ; -3) và chứa trục Oy thì (β) qua điểm O( 0 ; 0 ; 0) có (1 ; 4 ; -3) và
(0 ; 1 ; 0) là cặp vectơ chỉ phương.
Phương trình mặt phẳng (β) có dạng : 3x + z = 0.
c) Mặt phẳng (ɣ) qua điểm R(3 ; -4 ; 7) và chứa trục Oz chứa giá của các vectơ
(3 ; -4 ; 7) và
(0 ; 0 ; 1) nhận 2 vectơ này làm vectơ chỉ phương.
Phương trình mặt phẳng (ɣ) có dạng :4x + 3y = 0.
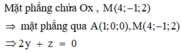
(P) chứa Ox và điểm P(4; -1; 2).
+ (P) chứa Ox ⇒ nhận i → = (1; 0; 0) là 1 vtcp
+ (P) chứa O(0 ; 0 ; 0) và P(4 ; -1 ; 2) ⇒ nhận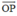
= ( 4 ; -1 ; 2) là 1 vtcp
⇒ (P) nhận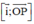
= (0; -2; -1) là 1 vtpt
⇒ (P): -2.(y – 0) – 1.(z – 0) = 0
hay (P) : 2y + z = 0.