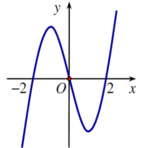
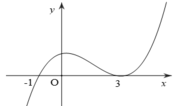
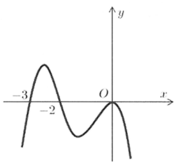
Cho hàm số f( x) xác định trên R và có đồ thị hàm số f’( x) là đường cong trong hình bên. Mệnh đề nào dưới đây đúng? A. Hàm số f( x) nghịch biến trên khoảng (-1;1) B. Hàm số f( x) đồng biến trên khoảng ( 1;2) C. Hàm số f( x) đồng biến trên khoảng ( -2 ;1) D. Hàm số f(x) nghịch biến trên khoảng (0; 2)...
Đọc tiếp
Cho hàm số f( x) xác định trên R và có đồ thị hàm số f’( x) là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?
A. Hàm số f( x) nghịch biến trên khoảng (-1;1)
B. Hàm số f( x) đồng biến trên khoảng ( 1;2)
C. Hàm số f( x) đồng biến trên khoảng ( -2 ;1)
D. Hàm số f(x) nghịch biến trên khoảng (0; 2) .
![{\max }\limits_{\left[ {1;2} \right]} f\left( x \right) = 2](http://cdn.hoc24.vn/bk/mzxhdszSooxT.png){kind=small}
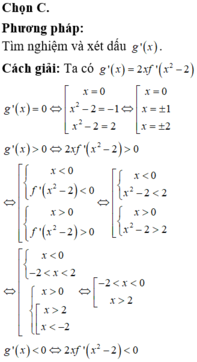
![{\max }\limits_{\left[ { - 2;1} \right]} f\left( x \right) = 0.](http://cdn.hoc24.vn/bk/rW9NnudP05Nm.png)
![{\max }\limits_{\left[ { - 3;0} \right]} f\left( x \right) = f\left( { - 3} \right)](http://cdn.hoc24.vn/bk/wAoYyWlWiYSj.png)
![{\max }\limits_{\left[ {3;4} \right]} f\left( x \right) = f\left( 4 \right)](http://cdn.hoc24.vn/bk/KAEY7gQbfMnd.png)
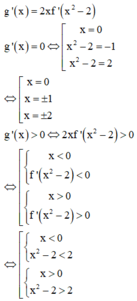
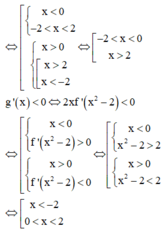
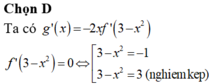
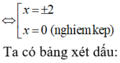
Chọn D
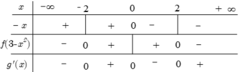
Quan sát đồ thị hàm số y= f’( x)
+ Trên khoảng (0; 2) ta thấy đồ thị hàm số y= f’( x) nằm bên dưới trục hoành.
=> Trên khoảng (0; 2) thì f’( x) < 0.
=> Hàm số y= f( x) nghịch biến trên khoảng ( 0; 2) .