Vẽ bán kính OM, đường kính AB trong hình tròn sau:

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

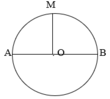

Học sinh tự nối tâm của đường tròn tới điểm bất kì trên đường biên của đường tròn ta được bán kính của đường tròn

Học sinh tự nối tâm của đường tròn tới điểm bất kì trên đường biên của đường tròn ta được bán kính của đường tròn

Sau khi vẽ ta được hình như sau:
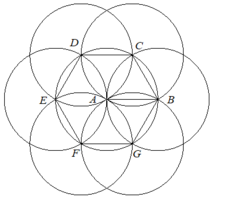
Khi đó, các đoạn thẳng A B = B C = C D = D E = E F = F G = G B (vì cùng bằng bán kính).

Sau khi vẽ ta được hình bs.17
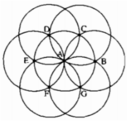
Khi đó, các đoạn thẳng: AB, BC, CD, EF, FG, GB bằng nhau (vì cùng bằng bán kính).

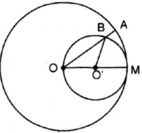
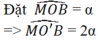 (góc nội tiếp và góc ở tâ của đường tròn (O'))
(góc nội tiếp và góc ở tâ của đường tròn (O'))
Độ dài cung M A ⏜ là:
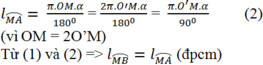

Xét (I) có
ΔADO nội tiếp
AO là đường kính
=>ΔADO vuông tại D
góc ADC=góc AHC=90 độ
=>AHDC nội tiếp
Xét ΔOHC vuông tại H và ΔODA vuông tại D có
OC=OA
góc HOC chung
=>ΔOHC=ΔODA
=>OH=OD
Xét ΔOAC có OH/OA=OD/OC
nên HD//AC
Xét tứ giác AHDC có
HD//AC
góc HAC=góc DCA
=>AHDC là hình thang cân

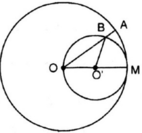

Kiến thức áp dụng
+ Trên đường tròn đường kính R, độ dài cung n0 bằng :
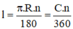

Vì 2 cung tròn cắt nhau tại M nên AM = MB = bán kính cung tròn
Chứng minh tương tự \( \Rightarrow \) AN = BN = bán kính cung tròn
\( \Rightarrow \) Vì M, N cách đều 2 đầu mút của đoạn AB nên M, N thuộc trung trực của AB
Và chỉ có 1 đường thẳng đi qua 2 điểm nên MN là trung trực của AB