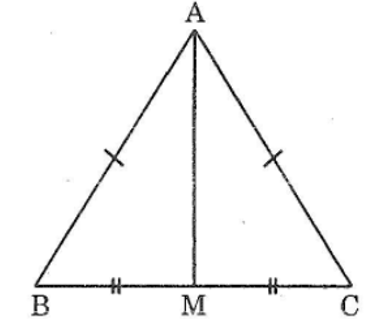
Cho △ABC có AB=AC. Gọi M là trung điểm của BC. Chứng minh rằng AM ⊥ (vuông góc) với BC
Giúp tui với ![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔAMB và ΔAMC, ta có:
AB = AC (gt)
BM = CM (vì M là trung điểm BC)
AM cạnh chung
Suy ra: ΔAMB= ΔAMC(c.c.c)
⇒ ∠(AMB) =∠(AMC) ̂(hai góc tương ứng)
Ta có: ∠(AMB) +∠(AMC) =180o (hai góc kề bù)
∠(AMB) =∠(AMC) =90o. Vậy AM ⏊ BC
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nen AM là đường cao

a) Xét `ΔABM` và `ΔACN` có:
`\hat{AMB}=\hat{ANC}=90^o`
`AB=AC(g t)`
`\hat{A}:chung`
`⇒ ΔABM=ΔΔACN(CH-GN)`
`=> AM=AN` (2 cạnh tương ứng)
b) Xét `ΔAHN` và `ΔAHM` có:
`AN=AM(cmt)`
`\hat{ANH}=\hat{AMH}=90^o`
`AH:chung`
`=> ΔAHN=ΔAHM(CH-CGV)`
`=> \hat{NAH}=\hat{MAH}` (2 góc tương ứng)
`=> AH` là tia phân giác của `\hat{NAM}` (hay `\hat{BAC}`) (1)
Xét `ΔABK` và `ΔACK` có:
`AB=AC(g t)`
`AK:chung`
`BK=KC` (K là trung điểm của BC)
`=> ΔABK=ΔACK(c.c.c)`
`=> \hat{BAK}=\hat{CAK}` (2 góc tương ứng)
`=> AK` là tia phân giác của `\hat{BAC}` (2)
Từ (1) và (2) `=>` 3 điểm `A,H,K` thẳng hàng
nguồn: copy

a) Xét \(\Delta ABC\)có
\(AB=AC\left(gt\right)\)
\(\Rightarrow\Delta ABC\)cân tại A
\(\Rightarrow\widehat{B}=\widehat{C}\)
b) Vì M là trung điểm của BC
=> AM là đường trung tuyến của \(\Delta ABC\)
Trong tam giác cân đường trung tuyến cũng là đường cao
\(\Rightarrow AM\perp BC\)
A B M C 1 2
a) Xét \(\Delta ABC\)có : AB = BC ( gt )
\(\Rightarrow\Delta ABC\)cân tại A
\(\Rightarrow\widehat{B}=\widehat{C}\)
b) Xét \(\Delta ABM\)và \(\Delta ACM\)có :
\(AB=AC\left(gt\right)\)
\(BM=MC\)( M là trung điểm của BC )
AM chung
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\)
\(\Rightarrow\widehat{M_1}=\widehat{M_2}\)( 2 góc tương ứng )
mà \(\widehat{M_1}+\widehat{M_2}=180^o\)( kề bù )
\(\Rightarrow\widehat{M_1}=90^o\)
\(\Rightarrow AM\perp BC\)

Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao

A B C H D M
Tam giác ABC cân tại A, H là trung điểm của BC nên \(AH\perp BC\).
Có \(\overrightarrow{AM}.\overrightarrow{BD}=\dfrac{1}{2}\left(\overrightarrow{AH}+\overrightarrow{AD}\right)\left(\overrightarrow{BH}+\overrightarrow{HD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{AH}.\overrightarrow{BH}+\overrightarrow{AH}.\overrightarrow{HD}+\overrightarrow{AD}.\overrightarrow{BH}+\overrightarrow{AD}.\overrightarrow{HD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{AH}.\overrightarrow{HD}+\overrightarrow{AD}.\overrightarrow{BH}\right)\) (do \(AH\perp BC\) )
\(=\dfrac{1}{2}\overrightarrow{AH}.\left(\overrightarrow{BH}+\overrightarrow{HD}\right)+\dfrac{1}{2}\left(\overrightarrow{AH}+\overrightarrow{HD}\right).\overrightarrow{BH}\)
\(=\dfrac{1}{2}\overrightarrow{AH}.\overrightarrow{BH}+\dfrac{1}{2}\overrightarrow{AH}.\overrightarrow{HD}+\dfrac{1}{2}\overrightarrow{AH}.\overrightarrow{BH}+\dfrac{1}{2}\overrightarrow{HD}.\overrightarrow{BH}\)
\(=\dfrac{1}{2}\overrightarrow{AH}.\overrightarrow{HD}+\dfrac{1}{2}\overrightarrow{HD}.\overrightarrow{BH}\) ( do \(AH\perp BC\) )
\(=\dfrac{1}{2}\overrightarrow{HD}\left(\overrightarrow{AH}+\overrightarrow{BH}\right)\)
\(=\dfrac{1}{2}\overrightarrow{HD}\left(\overrightarrow{AH}+\overrightarrow{HC}\right)\) ( doM là trung điểm của BC).
\(=\dfrac{1}{2}\overrightarrow{HD}.\overrightarrow{AC}\)
\(=0\) (Do \(HD\perp AC\) )
Xét tam giác AMB và tam giác AMC
Có: AB=AC (gt)
AM chung
MC=MB (B là trung điểm)
=>Tam giác AMB=tam giác AMC (c.c.c)
=>Góc AMB=góc AMC (2 góc tương ứng)
=>Góc AMB=góc AMC=90 độ
=>AM vuông góc với BC (đpcm)
Đây bạn nhé, chúc học tốt!!!
Xét △ ABC có AB=AC
⇒ △ ABC cân tại A
Vì M là trung điểm của BC
⇒ AM là đường trung tuyến
mà trong tam giác cân đường trung tuyến đồng thời là đường cao
⇒AM⊥BC