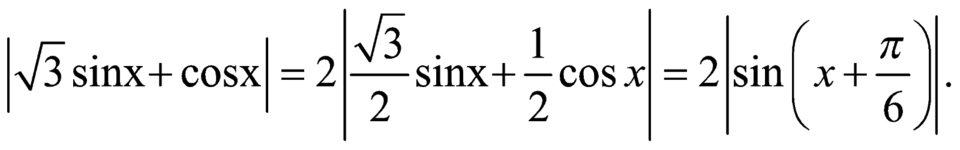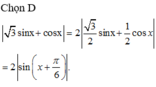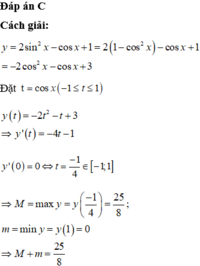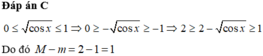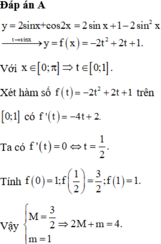Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Khi đó tích M.m bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

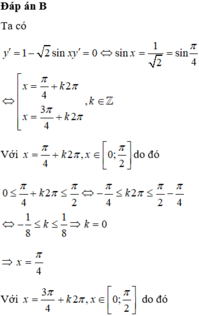
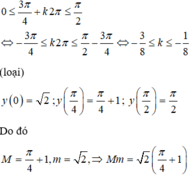

Đáp án C
Ta có y = - 1 + 2 - 3 . 2 sin x c o s x + 2 cos 2 x = 2 - 3 . sin 2 x + cos 2 x .
Áp dụng bất đẳng thức Bunhicopxki, có
2 - 3 . sin 2 x + cos 2 x 2 ≤ 2 - 3 2 + 1 2 . sin 2 2 x + cos 2 2 x = 8 - 4 3
Suy ra y 2 ≤ 8 - 4 3 ⇔ 8 - 4 3 ≤ y ≤ 8 - 4 3 . Vậy M + N + 2 = 2.

Đáp án C
Ta có: y = − 1 + 2 − 3 .2 sin x cos x + 2 cos 2 x
= 2 − 3 . sin 2 x + cos 2 x
Áp dụng bất đẳng thức Bunhiacopxki, có:
2 − 3 . sin 2 x + cos 2 x 2 ≤ 2 − 3 2 + 1 2 . sin 2 2 x + cos 2 2 x = 8 − 4 3
Suy ra y 2 ≤ 8 − 4 3 ⇔ − 8 − 4 3 ≤ y ≤ 8 − 4 3 .
Vậy M + N + 2 = 2

Đáp án A.
Điều kiện x ∈ ℝ
y = cos x + cos x − π 3 = cos x + cos x . cos π 3 + sin x . sin π 3 = cos x + 1 2 cos x + 3 2 sin x
= 3 2 cos x + 3 2 sin x
Cách 1: y = 3 3 2 cos x + 1 2 sin x = 3 sin x + π 3 Suy ra − 3 ≤ y ≤ 3
Vậy m = − 3 ; M = 3 và do đó M 2 + m 2 = 6
Cách 2:
Áp dụng bất đẳng thức Bunyakovsky ta có:
3 2 cos x + 3 2 sin x 2 ≤ 3 2 2 + 3 2 2 cos x 2 + sin x 2
⇔ 3 2 cos x + 3 2 sin x 2 ≤ 3 ⇔ − 3 ≤ y ≤ 3
⇒ M = 3 khi 2 3 cos x = 2 3 sin x 3 2 cos x + 3 2 sin x = 3
Tương tự ta có m = − 3 khi 2 3 cos x = 2 3 sin x 3 2 cos x + 3 2 sin x = − 3
⇒ M 2 + m 2 = 3 2 + − 3 2 = 6
Vậy ta chọn A.

Đáp án D
Ta có ![]() liên tục trên đoạn
liên tục trên đoạn ![]() .
.
Ta có ![]()
 .
.
![]() .
.
Vậy m=2 và M = 11, do đó ![]() .
.