Tìm khẳng định sai trong các khẳng định sau:
A. ∫ 0 1 sin 1 - x d x = ∫ 0 1 sinx d x
B. ∫ 0 π sin x 2 d x = 2 ∫ 0 π 2 sin x 2 d x
C. ∫ 0 1 1 + x x d x = 0
D. ∫ 0 1 x 2007 1 + x d x = 2 2009
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A, B, D đúng theo các tính chất của giá trị tuyệt đối, do đó C sai.
Đáp án: C

Các khẳng định là mệnh đề là:
a) \(3 + 2 > 5\)
d) \(1 - \sqrt 2 < 0\)
Các khẳng định là mệnh đề chứa biến là:
b) \(1 - 2x = 0\)
c) \(x - y = 2\)

Chọn B.
Dễ thấy (I) sai ( với x không thuộc tập xác định thì tại điểm đó hàm số gián đoạn)
Khẳng định (II) là lí thuyết.
Hàm số: ![]() liên tục trên khoảng (-3; 3). Liên tục phải tại 3 và liên tục trái tại -3.
liên tục trên khoảng (-3; 3). Liên tục phải tại 3 và liên tục trái tại -3.
Nên ![]() liên tục trên đoạn [-3; 3].
liên tục trên đoạn [-3; 3].

1. \(-19\le x\le20\)
Các số x thỏa là: \(x\in\left\{-19;-18;...;20\right\}\)
Tổng các chữ số đó là:
\(\left(-19\right)+\left(-18\right)+\left(-17\right)+...+19+20\)
\(=\left(19-19\right)+\left(18-18\right)+...+\left(1-1\right)+0+20\)
\(=20\)
2. Ta có
Khẳng định A đúng
Khẳng định B đúng
Khẳng định C đúng
Khẳng định D sai ⇒ số nguyên âm bé nhất có hai chữ số là - 99
⇒ Chọn đáp án D
3. Do trong hình chữ nhật thì độ dài của hai đường chéo bằng nhau
Mà có hình chữ nhật MNPQ nên MN, NP, PQ, MQ là các cạnh còn NQ và MP là đường chéo
⇒ NQ = MP = 6(cm)
⇒ Chọn đáp án C

Chọn A.
Với x >1 ta có hàm số f(x) = x2 liên tục trên khoảng (1; +∞). (1)
Với 0 < x < 1 ta có hàm số 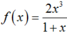 liên tục trên khoảng (0; 1). (2)
liên tục trên khoảng (0; 1). (2)
Với x < 0 ta có f(x) = x.sinx liên tục trên khoảng (-∞; 0). (3)
Với x = 1 ta có f(1) = 1; 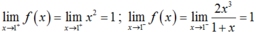
Suy ra ![]() .
.
Vậy hàm số liên tục tại x = 1.
Với x = 0 ta có f(0) = 0; 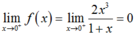 ;
;
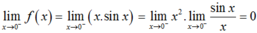 suy ra
suy ra ![]() .
.
Vậy hàm số liên tục tại x = 0. (4)
Từ (1), (2), (3) và (4) suy ra hàm số liên tục trên R.
Chọn A.

Đáp án C
Xét khẳng định C:
Nếu đường thẳng d đi qua gốc tọa độ O thì đường thẳng d có vectơ chỉ phương là OM → = (2; -1; 1)
Do u d → . n p → = 2.1 - 1.1 + 1.1 = 2 ≠ 0 nên đường thẳng d không song song với mặt phẳng (P)
(mâu thuẫn giả thiết)
Vậy khẳng định C là sai.

* Với m= 3 thì phương trình đã cho trở thành: x2 – 6x + 1= 0.
Phương trình này có 2 nghiệm x 1 = 3 + 2 2 ; x 2 = 3 - 2 2 nên x 1 - x 2 = 4 2
* Với m= 2 thì phương trình đã cho trở thành: x2 – 4x = 0.
Phương trình này có 2 nghiệm là x1 =0 và x2 = 4 nên |x1 – x2| = 4
* Với m= 1 thì phương trình đã cho trở thành: x2 – 2x - 1= 0.
Phương trình này có 2 nghiệm x 1 = 1 + 2 ; x 2 = 1 - 2 nên x 1 - x 2 = 2 2
* Phương trình đã cho có:
∆ ' = m 2 - m - 2 = m 2 - m + 2 = m 2 - 2 . 1 2 . m + 1 4 + 7 4 = m - 1 4 2 + 7 4 > 0 ∀ m
Do đó, không có giá trị nào của m để ∆’ = 0 hay không có giá trị nào của m để phương trình đã cho có nghiệm kép.
Chọn D.
Đáp án: D.
Hướng dẫn: Do 1 + x x ≥ 1 , ∀ x ∈ [0;1] nên nhờ ý nghĩa hình học của tích phân,
ta có: