Hình 98 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo (AO = OB).
Hãy so sánh tổng thể tích của hai hình nón và thể tích của hình trụ.
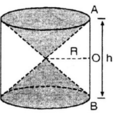
Hình 98
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
22 tháng 1 2018
Đúng(0)
Những câu hỏi liên quan
CM
27 tháng 8 2017
Đáp án D.
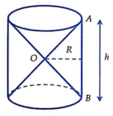
Do OA = OB nên chiều cao của hình nón bằng h 2
Tổng thể tích của 2 hình nón là:
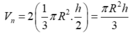
Thể tích hình trụ: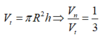 
CM
10 tháng 12 2018
Đáp án B
Gọi r , h , r ' , h ' lần lượt là bán kính và chiều cao của hình nón lớn và nhỏ
Phân tích dữ kiện
+) Chiều cao của đồng hồ là 30 cm ⇔ h + h ' = 30 c m
+) Tổng thể tích của đồng hồ là 1000 π c m 3
⇔ V l + V n = π r 2 h + π r ' 2 h ' 3 = 1000 π ⇔ r 2 h + r ' 2 h ' = 3000
+) Đường sinh bất kỳ của hình nón tạo với đáy một góc 60 ° ⇔ h r = h ' r ' = 3
Ta có hệ:
h + h ' = 3 r + r ' r 2 h + r ' 2 h ' = 3 r 3 + r ' 3 = 3000 ⇔ 3 r + r ' 3 = 9000 3 r 3 + r ' 3 = 3000 ⇔ r + r ' 3 r 3 + r ' 3 = 3
⇔ 2 r ' 2 − 5 r r ' + 2 r 2 = 0 ⇔ r r ' = 1 2
vì 0 < r ' < r
Theo đó tỉ lệ cần tính là:
V n V l = r ' 2 h ' r 2 h = r ' r 3 = 1 8
PT
1
CM
8 tháng 6 2019
Thể tích cần tính gồm một hình trụ và hai nửa hình cầu.
- Hình cầu có đường kính d = 1,8m ⇒ bán kính R = 0,9m
- Hình trụ có bán kính đáy bằng bán kính hình cầu R = 0,9m; chiều cao h = 3,62m.
Thể tích hình trụ: V 1 = π ⋅ R 2 ⋅ h ≈ 9 , 21 m 3
Thể tích hai nửa hình cầu: V 2 = 4 3 π ⋅ R 3 ≈ 3 , 05 m 3
Thể tích bồn chứa xăng: V = V 1 + V 2 ≈ 12 , 26 m 3