Cho biểu thức P = x(x – y) y(x y) – y 2 . Khẳng định nào sau đây là đúng?A. Giá trị biểu thức P không phụ thuộc vào giá trị của x và y.B. Giá trị biểu thức P phụ thuộc vào giá trị của x và yC. Giá...

MA

Mập ak

13 tháng 11 2021

Cho biểu thức P = x(x – y) + y(x + y) – y 2 . Khẳng định nào sau đây là đúng?A. Giá trị biểu thức P không phụ thuộc vào giá trị của x và y.B. Giá trị biểu thức P phụ thuộc vào giá trị của x và yC. Giá trị biểu thức P chỉ phụ thuộc vào giá trị của x.D. Giá trị biểu thức P chỉ phụ thuộc vào giá trị của...

Đọc tiếp

#Toán lớp 8

4

NH

Nguyễn Hoàng Minh

13 tháng 11 2021

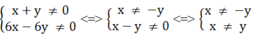
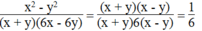
\(P=x^2-xy+xy+y^2-y^2=x^2\)

Vậy chọn C

Đúng(0)

NT

nguyễn thị hương giang

13 tháng 11 2021

Cho biểu thức P = x(x – y) + y(x + y) – y 2 . Khẳng định nào sau đây là đúng?

A. Giá trị biểu thức P không phụ thuộc vào giá trị của x và y.

B. Giá trị biểu thức P phụ thuộc vào giá trị của x và y

C. Giá trị biểu thức P chỉ phụ thuộc vào giá trị của x.

D. Giá trị biểu thức P chỉ phụ thuộc vào giá trị của y.

Bài làm:

\(P=x\left(x-y\right)+y\left(x+y\right)-y^2\)

\(=x^2-xy+xy+y^2-y^2\)

\(=x^2\)

Vậy biểu thức P chỉ phụ thuộc vào giá trị x.

Chọn C.

Đúng(0)

E

evangelion

19 tháng 9 2021

Cho biểu thức B=-x(x-y)-y(x+y)+(x+y)(x-y)+2y^(2).Chứng minh rằng giá trị của biểu thức B không phụ thuộc vào giá trị của biến.

#Toán lớp 8

2

PA

Phan An

19 tháng 9 2021

B=-x(x-y)-y(x+y)+(x+y)(x-y)+2y^(2)

B=-x^2+xy-yx-y^2+x^2-xy+xy-y^2+2y^2

B=0

vậu B ko phọ thuộc vào gt của biến

Đúng(1)

NL

Nguyễn Lê Phước Thịnh

19 tháng 9 2021

\(B=-x\left(x-y\right)-y\left(x+y\right)+\left(x+y\right)\left(x-y\right)+2y^2\)

\(=-x^2+xy-xy-y^2+x^2-y^2+2y^2\)

=0

Đúng(1)

PT

Pham Trong Bach

11 tháng 5 2018

Chứng mình rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến y (x≠0; y≠0) với biểu thức đó là A = 2 3 x 2 y 3 : - 1 3 x y + 2 x ( y - 1 ) ( y + 1 )

#Toán lớp 8

1

CM

Cao Minh Tâm

11 tháng 5 2018

Đúng(0)

PT

Pham Trong Bach

28 tháng 6 2018

Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến y (x≠0; y≠0) với biểu thức đó là A = 2 3 x 2 y 3 : - 1 3 x y + 2 x ( y - 1 ) ( y + 1 )

#Toán lớp 8

1

CM

Cao Minh Tâm

28 tháng 6 2018

Đúng(0)

TT

thuyhang tran

20 tháng 9 2021

2 rút gọn giá trị biểu thức ( dạng 2 : chứng tỏ biểu thức ko phụ thuộc vào giá trị của biến )a, P = ( 2x + 1 ) ( 4x^2 - 2x + 1 ) tại x = 1/2 b, Q = ( X + 3y ) ( x^2 - 3xy + 9y^2 ) tại x = 1 và y = 1/33 chứng minh giá trị của biểu thức sau ko phụ thuộc vào giá trị của biến ( dạng 3 : tìm x biết x thỏa mãn điều kiện cho trc ) 4 tìm x ( dạng 4 : chứng minh đẳng thức ) ( 8x + 2 ) ( 1 - 3x ) + ( 6x - 1) ( 4x - 10 ) =...

Đọc tiếp

#Toán lớp 8

1

LL

Lấp La Lấp Lánh

20 tháng 9 2021

2) \(P=\left(2x+1\right)\left(4x^2-2x+1\right)=8x^3+1=8.\left(\dfrac{1}{2}\right)^3+1=8.\dfrac{1}{8}+1=2\)

\(Q=\left(x+3y\right)\left(x^2-3xy+9y^2\right)=x^3+27y^3=1^3+27.\left(\dfrac{1}{3}\right)^3=1+27.\dfrac{1}{27}=2\)

3) \(\left(8x+2\right)\left(1-3x\right)+\left(6x-1\right)\left(4x-10\right)=-50\)

\(\Leftrightarrow-24x^2+2x+2+24x^2-64x+10=-50\)

\(\Leftrightarrow-62x=-62\Leftrightarrow x=1\)

Đúng(2)

NQ

Nguyễn Quỳnh Anh

31 tháng 10 2023 - olm

b) Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến 2 và y: E = (2x - y) ^ 3 + (3x + y) ^ 2 + 2(2x - y)(3x + y) - 25(1 + x)(x - 1)

#Toán lớp 8

1

KV

Kiều Vũ Linh

31 tháng 10 2023

Sửa đề:

E = (2x - y)² + (3x + y)² + 2(2x - y)(3x + y) + 25(1 + x)(1 - x)

= (2x - y + 3x + y)² + 25 - 25x²

= (5x)² + 25 - 25x²

= 25x² + 25 - 25x²

= 25

Vậy giá trị của E không phụ thuộc vào giá trị của x và y

Đúng(1)

PT

Pham Trong Bach

28 tháng 6 2019

Tìm điều kiện của các biến trong mỗi phân thức sau đây. Chứng minh rằng khi giá trị của phân thức xác định thì giá trị đó không phụ thuộc vào các biến x và y (nghĩa là chứng tỏ rằng có thể biến đổi phân thức đã cho thành một biểu thức không chứa x và y) x 2 - y 2 x + y 6 x - 6 y ...

Đọc tiếp

#Toán lớp 8

1

CM

Cao Minh Tâm

28 tháng 6 2019

xác định khi:

(x + y)(6x – 6y) ≠ 0 ⇒ Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Điều kiện x ≠ ± y

Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Vậy biểu thức không phụ thuộc vào x, y.

Đúng(0)

SP

shoppe pi pi pi pi

8 tháng 10 2018 - olm

a/chứng minh rằng biểu thức sau không âm với mọi giá trị của biến
A=(-15.x^3.y^6):(-5xy^2)
b/chứng minh rằng giá trị biểu thức sau ko phụ thuộc vào giá trị của biến y(x,y khác 0)
B=2/3 x^2 y^3:(-1/3xy)+2x(y-1)(y+1)

#Toán lớp 8

0

TU

Tạ Uy Vũ

2 tháng 11 2023 - olm

: Chứng minh rằng các biểu thức sau có giá trị không phụ thuộc vào giá trị của biến. A = (x – 2y)(x + 2y) + (2y – x)2 + 2023 + 4xy B = ( 2x - 3 )(x - y) - (x - y)2 + (y - x)(x +...

Đọc tiếp

#Toán lớp 8

3

H9

HT.Phong (9A5)

CTVHS

2 tháng 11 2023

\(A=\left(x-2y\right)\left(x+2y\right)+\left(2y-x\right)^2+2023+4xy\)

\(A=x^2-\left(2y\right)^2+\left(4y^2-4xy+x^2\right)+2023+4xy\)

\(A=x^2-4y^2+4y^2-4xy+x^2+4xy\)

\(A=2x^2+2023\)

Vậy giá trị của biểu thức chỉ phụ thuộc vào x không phụ thuộc vào y

\(B=\left(2x-3\right)\left(x-y\right)-\left(x-y\right)^2+\left(y-x\right)\left(x+y\right)\)

\(B=2x^2-2xy-3x+3y-\left(x^2-2xy+y^2\right)+y^2-x^2\)

\(B=2x^2-2xy-3x+3y-x^2+2xy-y^2+y^2-x^2\)

\(B=-3x+3y\)

Vậy giá trị của biểu thức vẫn phụ thuộc vào biến

Đúng(1)

NT

Nguyễn Thị Thương Hoài

Giáo viên VIP

2 tháng 11 2023

A = (\(x\) - 2y)(\(x\) + 2y) + (2y - \(x\))² + 2023 + 4\(xy\)

A = \(x^2\) - 4y² + 4y² - 4\(xy\) + \(x^2\) + 2023 + 4\(xy\)

A = (\(x^2\) + \(x^2\)) - (4y² - 4y²) + 2023 - (4\(xy\) - 4\(xy\))

A = 2\(x^2\) - 0 + 2023 - 0

A = 2\(x^2\) + 2023

Việc chứng minh A có giá trị không phụ thuộc vào giá trị của biến là điều không thể xảy ra.

Đúng(0)

TT

thuyhang tran

20 tháng 9 2021

2 rút gọn giá trị biểu thức

a, P = ( 2x + 1 ) ( 4x^2 - 2x + 1 ) tại x = 1/2

b, Q = ( X + 3y ) ( x^2 - 3xy + 9y^2 ) tại x = 1 và y = 1/3

3 chứng minh giá trị của biểu thức sau ko phụ thuộc vào giá trị của biến

4 tìm x

( 8x + 2 ) ( 1 - 3x ) + ( 6x - 1) ( 4x - 10 ) = -50

giúp mik với mik cần gấp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

20 tháng 9 2021

Bài 4:

Ta có: \(\left(8x+2\right)\left(1-3x\right)+\left(6x-1\right)\left(4x-10\right)=-50\)

\(\Leftrightarrow8x-24x^2+2-6x+24x^2-60x-4x+40=-50\)

\(\Leftrightarrow-62x=-92\)

hay \(x=\dfrac{46}{31}\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP