Trong tất cả các hình chóp tứ giác đều có d= 3 là khoảng cách giữa hai đường thẳng chéo nhau gồm một đường thẳng chứa một đường chéo của đáy và đường thẳng còn lại chứa một cạnh bên hình chóp. Thể tích nhỏ nhất V m i n của khối chóp là
A. V m i n =3
B. V m i n =9
C. V m i n = 9 3
D. V m i n =27


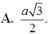
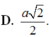
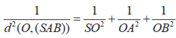
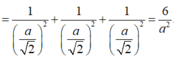
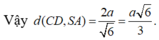

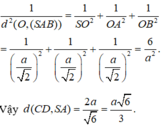
Chọn B.
Lời giải.
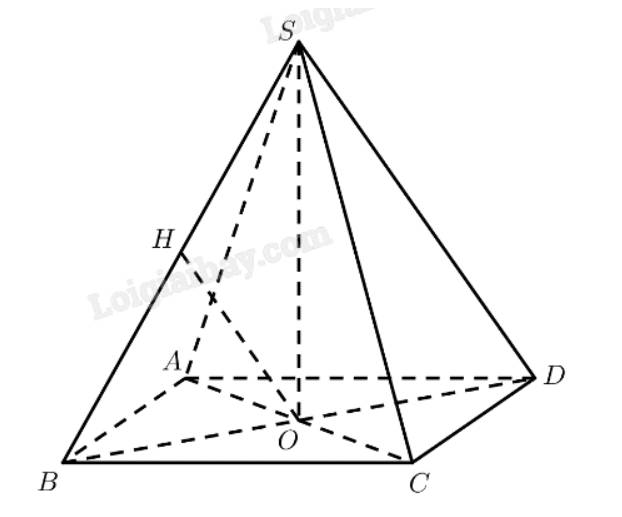
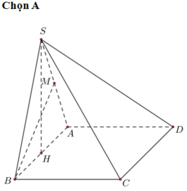
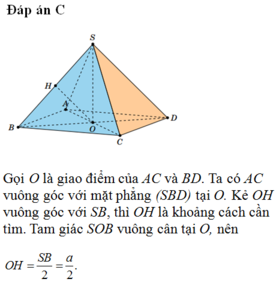
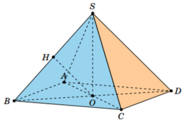
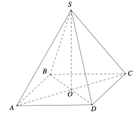
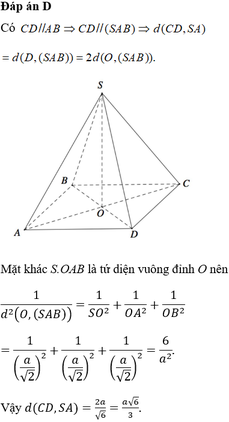
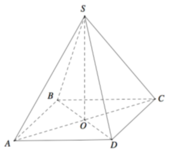
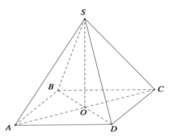
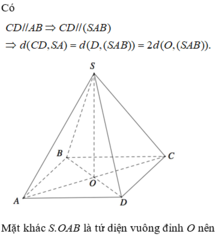
Xét hình chóp tứ giác đều S.ABCD, đặt AB =x, SO =h. Với O là tâm của hình vuông ABCD ⇒ S O ⊥ ( A B C D ) . Qua O kẻ đường thẳng OH vuông góc với SA với H ∈ SA
Ta có
Suy ra OH là đoạn vuông góc chung của SA và BD
Theo bài ra, ta có
Tam giác SAO vuông tại O, có đường cao OH suy ra