Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, BC = a 2 và góc giữa A’B và mặt phẳng (ABC) là 60o. Bán kính của mặt cầu ngoại tiếp lăng trụ là:
A. 2a
B. a 5 2
C. a 3 2
D. a 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 3 2019
Đáp án C
Tam giác ABC vuông tại A ⇒ B C = A B 2 + A C 2 = 2 a ⇒ R Δ A B C = B C 2 = a
Bán kính mặt cầu ngoại tiếp khối lăng trụ là R = R 2 Δ A B C + A A ' 2 4 = a 2 + 2 a 2 4 = a 2 .
CM
28 tháng 5 2019
Chọn D
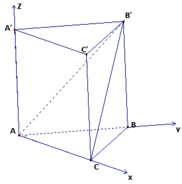
Vì tam giác ABC vuông cân tại A, cạnh BC = a√6 nên AB = AC = a√3.
Chọn hệ trục tọa độ Oxyz sao cho A (0;0;0), B (0; a√3; 0), C (a√3;0;0), A' (0;0;z) (z > 0).
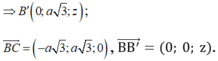
VTPT của (BCC'B') là:
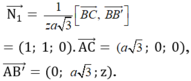
VTPT của mặt phẳng (BA'C) là:
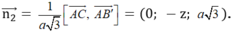
Vì góc giữa mặt phẳng và mặt phẳng bằng nên:
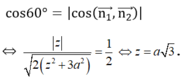
Vậy thể tích của khối lăng trụ ABC.A'B'C' là:
CM
6 tháng 2 2018
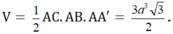
Đáp án D
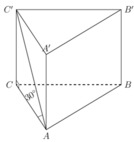
AC là hình chiếu của AC' trên (ABC) nên góc giữa AC' và (ABC) là 
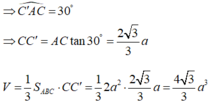
Đáp án B
Trong tam giác vuông ABC ta có
=> AA' = AB.tan60o = a√3.
Gọi I là tâm của hình chữ nhật BCC’B’ và M là trung điểm của BC. Do tam giác ABC vuông tại A nên M là tâm đường tròn ngoại tiếp tam giác ABC và do đó IM là trục của đường tròn ngoại tiếp đáy ABC và I cách đều B, B’ nên I là tâm của mặt cầu ngoại tiếp lăng trụ. Khi đó ta có: