Chia hình chóp tứ giác đều thành tám hình chóp bằng nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
1
CM
28 tháng 11 2018
Đáp án A.
Gọi cạnh đáy của khối chóp là x với
0 < x < 5 2 2 .
Chiều cao của khối chóp là
h = 5 2 2 − x 2 2 − x 2 2 = 25 − 5 x 2 2 .
Vậy thể tích của khối chóp là
V = 1 3 . h . S = 1 3 . x 2 . 25 − 5 x 2 2 = 1 3 25 x 4 − 5 x 5 2 2 .
Xét hàm số f x = 25 x 4 − 5 x 5 2 trên 0 ; 5 2 2 ,
ta có f ' x = 100 x 3 − 25 x 4 2 = 0 ⇔ x = 2 2 .
Suy ra giá trị lớn nhất của thể tích là V = 1 3 . f 2 2 2 = 4 10 3 .
31 tháng 7 2023
Sxq=1/2*40*13=20*13=260cm2
Độ dài cạnh ở đáy là 40/4=10cm
V=10^2*12=1200cm3
7 tháng 9 2023
Sxq=1/2*10*4*12=2*10*12=2*120=240cm2
Stp=240+10^2=340cm2
21 tháng 7 2023
a: Đúng
b: Sai. Hình chóp tứ giác đều có các cạnh bên bằng nhau và các cạnh đáy bằng nhau
31 tháng 7 2023
Sxq=16*4*17/2=544cm2
Stp=544+16^2=800cm2
V=1/3*16^2*15=1280cm3
H9
HT.Phong (9A5)
CTVHS
31 tháng 7 2023
Nữa chu vi đáy của hình chóp đều:
\(16\cdot4:2=32\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=32\cdot17=544\left(cm^2\right)\)
Diện tích mặt đáy của hình chóp đều:
\(S_đ=16^2=256\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=544+256=800\left(cm^2\right)\)
Thể tích của hình chóp đều:
\(V=\dfrac{1}{3}\cdot256\cdot15=1280\left(cm^3\right)\)
CM
2 tháng 2 2018
Bài giảng học thử
Video không hỗ trỡ trên thiết bị của bạn!
Bài 9: Hình chữ nhật - Phần 1 - Toán 8 - Cô Diệu Linh
27:4
Video không hỗ trỡ trên thiết bị của bạn!
Bài 1. Định lí Ta-lét trong tam giác - Phần 1 - Toán 8 - Thầy Phan Toàn
1:36
Video không hỗ trỡ trên thiết bị của bạn!
Bài 4. Đường trung bình của tam giác, của hình thang - Phần 2 - Toán 8 - Thầy Phan Toàn
11:21
Video không hỗ trỡ trên thiết bị của bạn!
Bài 3. Hình thang cân - Phần 3 - Toán 8 - Thầy Phan Toàn
11:28
Video không hỗ trỡ trên thiết bị của bạn!
Bài 4. Khái niệm hai tam giác đồng dạng - Phần 2 - Toán 8 - Thầy Phan Toàn
10:6
Xem thêm các bài giảng khác »
CM
26 tháng 3 2017
Đáp án B.
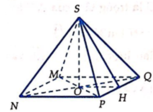
Sau khi cắt miếng giấy hình vuông như hình vẽ, ta xếp lại được thành hình chóp tứ giác đều S.MNPQ (hình bên).
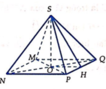Ta có
O
M
=
x
⇒
M
P
=
M
Q
=
20
M
=
2
x
=
M
N
2
⇒
M
N
=
2
x
(cm).
Gọi H là trung điểm P Q ⇒ O H = M N 2 = 2 x 2 (cm) và S H = 10 2 - 2 x 2 (cm).
Suy ra S O = S H 2 - O H 2 = 10 2 - 2 x 2 2 - 2 x 2 2 = 20 ( 10 - x ) .
Thể tích khối chóp S.MNPQ là:
V
M
N
P
Q
=
1
3
.
S
O
.
S
M
N
P
Q
=
1
3
20
(
10
-
x
)
.
2
x
2
=
20
3
(
40
-
4
x
)
.
x
4
→
V
M
N
P
Q
=
20
3
(
40
-
4
x
)
.
x
.
x
.
x
.
x
≤
20
3
40
-
4
x
+
x
+
x
+
x
+
x
5
=
256
10
3
Dấu “=” xảy ra ⇔ 40 - 4 x = x ⇔ x = 8 (cm).
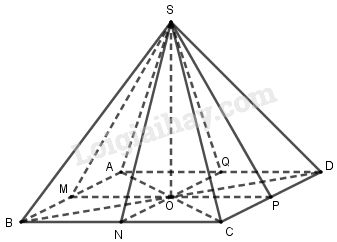
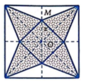
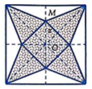
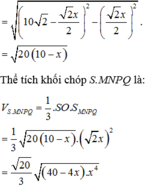
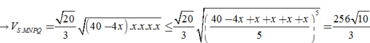
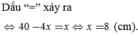
Cho hình chóp tứ giác đều S.ABCD. Hai đường chéo AC, BD và hai đường thẳng nối trung điểm các cặp cạnh đối diện của hình vuông ABCD chia hình vuông ABCD thành tám tam giác bằng nhau. Xem mỗi tam giác đó là đáy của một hình chóp đỉnh S ta sẽ được tám hình chóp bằng nhau.