Cho phân số a b a , b ∈ ℕ , b ≠ 0
Giả sử a b < 1 và m ∈ ℕ , m ≠ 0 . Chứng minh rằng: a b < a + m b + m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Thực hiện quy đồng a b = a ( b + m ) b ( b + m ) = a b + a m b 2 + b m ;
a + m b + m = b ( a + m ) b ( b + m ) = a b + b m b 2 + b m . Vì a b < 1=> a < b => ab +am < ab + bm
Từ đó thu được a b < a + m b + m
b) 437 564 < 437 + 9 564 + 9 = 446 573 .

Bài làm:
a) Vì \(\frac{13}{15}< 1\)\(\Rightarrow\frac{13}{15}< \frac{13+11}{15+11}=\frac{24}{26}\)
b) Vì \(\frac{13}{15}< 1\)\(\Rightarrow\frac{13}{15}< \frac{13+10}{15+10}=\frac{23}{25}\)
c) Vì \(\frac{3}{5}< 1\)\(\Rightarrow\frac{3}{5}< \frac{3+30}{5+30}=\frac{33}{35}\)
Học tốt!!!!
1 lớp học có 2 học sinh một bạn bị chết hỏi còn bao nhiêu bạn

Ta có: 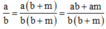
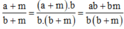
Ta có: a/b > 1 nên a > b suy ra am > bm, suy ra ab + am > ab + bm.
Do đó 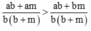
Hay 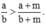

Câu 1: Giải
\(\frac{a}{b}< 1\Leftrightarrow a< b\)
\(\Leftrightarrow am< bm\)
\(\Leftrightarrow ab+am< ab+bm\)
\(\Leftrightarrow a\left(b+m\right)< b\left(a+m\right)\)
\(\Leftrightarrow\frac{a}{b}< \frac{a+m}{b+m}\left(đpcm\right)\)
Câu 2: Giải
Ta có : \(\hept{\begin{cases}\frac{437}{564}=1-\frac{127}{564}\\\frac{446}{573}=1-\frac{127}{573}\end{cases}}\)
Vì \(\frac{127}{564}>\frac{127}{573}\) nên \(\frac{437}{564}>\frac{446}{573}\)
Thực hiện quy đồng: a b = a b + m b b + m = a b + a m b 2 + b m
a + m b + m = b a + m b b + m = a b + b m b 2 + b m
Vì a b < 1 ⇒ a < b ⇒ a b + a m < a b + b m
Từ đó ta thu được a b < a + m b + m