Dựng tam giác ABC, biết BC = 4cm, góc A = 60 ° , bán kính đường tròn nội tiếp tam giác bằng 1cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


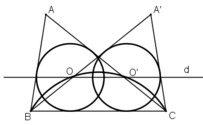
Phân tích:
Giả sử dựng được ΔABC thỏa mãn điều kiện.
Gọi O là tâm đường tròn nội tiếp tam giác.
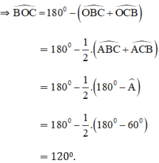
⇒ O thuộc cung m chứa góc 120 º dựng trên đoạn BC.
+ Bán kính đường tròn nội tiếp ΔABC bằng 1
⇒ O cách BC 1cm
⇒ O thuộc d // BC và cách BC 1cm.
Vậy O là giao của cung m và đường thẳng d.
+ Khi đó ta dựng được đường tròn (O; 1) nội tiếp ΔABC
⇒ A là giao của tiếp tuyến đi qua B và C của đường tròn (O; 1).
Cách dựng:
+ Dựng BC = 4cm
+ Dựng đường thẳng (d) song song với BC và cách BC một khoảng là 1 cm.
+ Dựng cung m chứa góc 120 º trên đoạn BC.
+ (d) cắt cung m tại O.
+ Dựng đường tròn tâm O, bán kính 1cm.
+ Kẻ tiếp tuyến từ B và C đến (O; 1cm).
Hai tiếp tuyến cắt nhau tại A.
ΔABC là tam giác cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 4cm .
+ O thuộc cung 120º dựng trên đoạn BC
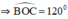
+ A là giao của 2 tiếp tuyến
⇒ (O; 1cm) tiếp xúc với AB và AC
Mà khoảng cách từ O đến BC = 1cm
⇒ (O; 1cm) cũng tiếp xúc với BC
⇒ (O; 1cm) là đường tròn nội tiếp ΔABC
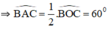
Vậy ΔABC có BC = 4cm, 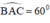 , đường tròn nội tiếp có bán kính 1cm thỏa mãn yêu cầu.
, đường tròn nội tiếp có bán kính 1cm thỏa mãn yêu cầu.
Biện luận:
Vì d cắt m tại hai điểm nên bài toán có hai nghiệm hình ΔABC và ΔA’BC như hình vẽ.

Hướng dẫn làm bài:
Dựng BC = 4cm và đường thẳng (d) song song với BC và cách BC một khoảng là 1cm
Tâm O của đường tròn nội tiếp ∆ABC là giao điểm của đường thẳng (d) với cung chứa góc 90° + 60° : 2 = 120° dựng trên đoạn BC cố định
Qua B và C vẽ các tiếp tuyến với (O), chúng cắt nhau tại A. Tam giác ABC là tam giác phải dựng
Dựng BC = 4cm và đường thẳng (d) song song với BC và cách BC một khoảng là 1 cm.
Tâm O của đường tròn nội tiếp tam giác ABC là giao điểm của đường thẳng (d) với cung chứa góc 90o + 60o : 2 = 120o dựng trên đoạn BC cố định.
Qua B và C vẽ các tiếp tuyến với (O), chúng cắt nhau tại A.
Tam giác ABC là tam giác cần dựng.

a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=1\cdot4=4\)
=>\(AH=\sqrt{4}=2\left(cm\right)\)
BC=BH+CH
=>BC=1+4=5(cm)
XétΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB^2=1\cdot5=5\\AC^2=4\cdot5=20\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{5}\left(cm\right)\\AC=2\sqrt{5}\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{\sqrt{5}}{5}\)
nên \(\widehat{C}\simeq27^0\)
ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=90^0-27^0=63^0\)
b: AH=2cm
=>H thuộc (A;2cm)
Xét (A;2cm) có
AH là bán kính
BC\(\perp\)AH tại H
Do đó: BC là tiếp tuyến của (A;2cm)
c: Sửa đề: BDEH
Xét ΔAHB vuông tại H và ΔADE vuông tại D có
AH=AD
\(\widehat{HAB}=\widehat{DAE}\)
Do đó: ΔAHB=ΔADE
=>HB=DE
Xét tứ giác BDEH có
BH//ED
BH=ED
Do đó: BDEH là hình bình hành
Phân tích:
Giả sử dựng được ΔABC thỏa mãn điều kiện.
Gọi O là tâm đường tròn nội tiếp tam giác.
⇒ O thuộc cung m chứa góc 120º dựng trên đoạn BC.
+ Bán kính đường tròn nội tiếp ΔABC bằng 1
⇒ O cách BC 1cm
⇒ O thuộc d // BC và cách BC 1cm.
Vậy O là giao của cung m và đường thẳng d.
+ Khi đó ta dựng được đường tròn (O; 1) nội tiếp ΔABC
⇒ A là giao của tiếp tuyến đi qua B và C của đường tròn (O; 1).
Cách dựng:
+ Dựng BC = 4cm
+ Dựng đường thẳng (d) song song với BC và cách BC một khoảng là 1 cm.
+ Dựng cung m chứa góc 120º trên đoạn BC.
+ (d) cắt cung m tại O.
+ Dựng đường tròn tâm O, bán kính 1cm.
+ Kẻ tiếp tuyến từ B và C đến (O; 1cm).
Hai tiếp tuyến cắt nhau tại A.
ΔABC là tam giác cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 4cm .
+ O thuộc cung 120º dựng trên đoạn BC
+ A là giao của 2 tiếp tuyến
⇒ (O; 1cm) tiếp xúc với AB và AC
Mà khoảng cách từ O đến BC = 1cm
⇒ (O; 1cm) cũng tiếp xúc với BC
⇒ (O; 1cm) là đường tròn nội tiếp ΔABC
Vậy ΔABC có BC = 4cm,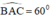 , đường tròn nội tiếp có bán kính 1cm thỏa mãn yêu cầu.
, đường tròn nội tiếp có bán kính 1cm thỏa mãn yêu cầu.
Biện luận:
Vì d cắt m tại hai điểm nên bài toán có hai nghiệm hình ΔABC và ΔA’BC như hình vẽ.