Chứng minh rằng sin 2(x + kπ) = sin 2x với mọi số nguyên k. Từ đó vẽ đồ thị hàm số y = sin 2x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 7 2018
a) + Hàm số y = cos x có chu kì 2π.
Do đó: cos 2.(x + kπ) = cos (2x + k2π) = cos 2x.
⇒ Hàm số y = cos 2x cũng tuần hoàn với chu kì π.
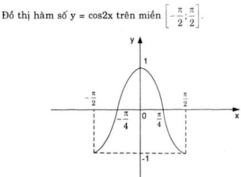
Từ đó suy ra
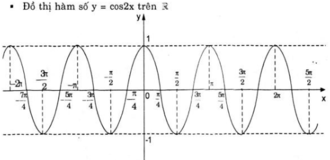
b. y = f(x) = cos 2x
⇒ y’ = f’(x) = (cos 2x)’ = -(2x)’.sin 2x = -2.sin 2x.
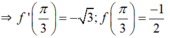
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3 là:
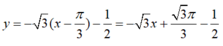
c. Ta có: 1 – cos 2x = 2.sin2x ≥ 0.
Và 1 + cos22x > 0; ∀ x
⇒ 
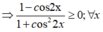
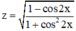luôn xác định với mọi x ∈ R.
CM
21 tháng 8 2018
cos2(x + kπ) = cos(2x + k2π) = cos2x, k ∈ Z.
Vậy hàm số y = cos 2x là hàm số chẵn, tuần hoàn, có chu kì là π.
Đồ thị hàm số y = cos2x
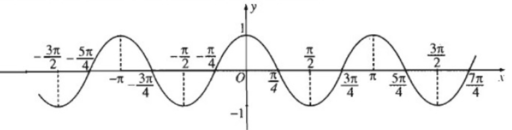
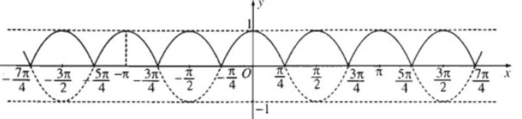
Đồ thị hàm số y = |cos2x|
CM
7 tháng 8 2019
Đáp án C
Hàm số y = sin 2x thỏa mãn tính chất trên, các hàm số y = tan x, y = cot x cần điều kiện của x.
+ sin 2x (x + kπ) = sin (2x + k2π) = sin 2x, (k ∈ Z)
(Do hàm số y = sin x có chu kì 2π).
⇒ Hàm số y = sin 2x tuần hoàn với chu kì π.
+ Hàm số y = sin 2x là hàm số tuần hoàn với chu kì π và là hàm số lẻ.
Bảng biến thiên hàm số y = sin 2x trên [-π/2; π/2]
Đồ thị:
Đồ thị hàm số y = sin 2x.