Chứng minh rằng: 1 3 2 5 < 1 3 3 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
25 tháng 7 2019
Đúng(0)
Những câu hỏi liên quan
16 tháng 11 2018
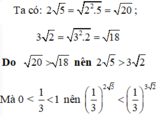
1:\(A=1+3+3^2+3^3+...+3^{11}\)
\(A=\left(1+3\right)+\left(3^2+3^3\right)+...+\left(3^{10}+3^{11}\right)\)
\(A=4+3^2\cdot\left(1+3\right)+...+3^{10}\cdot\left(1+3\right)\)
\(A=4+3^2\cdot4+....+3^{10}\cdot4\)
\(A=4\cdot\left(1+3^2+...+3^{10}\right)\) chia hết cho 4
Vì ta có 4 chia hết cho 4 => A có chia hết cho 4
Vậy A chia hết cho 4
16 tháng 11 2018
2:
\(C=5+5^2+5^3+...+5^8\) chia hết cho 30
\(C=\left(5+5^2\right)+...+\left(5^7+5^8\right)\)
\(C=30+5^2\cdot\left(5+5^2\right)+...+5^6\cdot\left(5+5^2\right)\)
\(C=30\cdot1+5^2\cdot30+...5^6\cdot30\)
\(C=30\cdot\left(5^2+...+5^6\right)\)
Vì ta có 30 chia hết cho 30 nên suy ra C có chia hết cho 30
Vậy C có chia hết cho 30
3 tháng 9 2017
a>
\(\frac{1}{2^2}+\frac{1}{100^2}\)=1/4+1/10000
ta có 1/4<1/2(vì 2 đề bài muốn chứng minh tổng đó nhỏ 1 thì chúng ta phải xét xem có bao nhiêu lũy thừa hoặc sht thì ta sẽ lấy 1 : cho số số hạng )
1/100^2<1/2
=>A<1
26 tháng 11 2015
1) \(5+5^2+5^3+.....+5^{12}=\left(5+5^2\right)+\left(5^3+5^4\right)+...+\left(5^{11}+5^{12}\right)\)
\(=30.1+5^2.30+.....+5^{10}.30=30.\left(1+5^2+....+5^{10}\right)\)
Vậy chia hết cho 30
\(5+5^2+5^3+....+5^{12}=\left(5+5^2+5^3\right)+.....+\left(5^{10}+5^{11}+5^{12}\right)\)
\(=5.31+5^4.31+....+5^{10}.31=31.\left(5+5^4+....+5^{10}\right)\)
Vậy chia hết cho 31
8 tháng 8 2016
Bài 1
a) 34 + 35 + 36 + 37 = 34(1 + 3 + 32 + 33)\
b) a)A = 1 + 3 + 32 +......399 =(1 + 3 + 32 + 33 ) + ...+(396 + 397 + 398 + 399)
= (1 + 3 + 32 + 33 ) + .. +396(1 + 3 + 32 + 33 )
= 40 + ... + 396 . 40
= 40 (1 + 3 +...+ 396) chia hết cho 40
8 tháng 8 2016
Bài 2
a)
+)A chia hết cho 6
\(A=5+5^2+5^3+...+5^{2004}\)
\(A=\left(5+5^2\right)+\left(5^3+5^4\right)+...+\left(5^{2003}+5^{2004}\right)\)
\(A=\left(5+5^2\right)+5^2\left(5+5^2\right)+...+5^{2002}\left(5+5^2\right)\)
\(A=30+5^2.30+...+5^{2002}.30\)
\(A=30\left(1+5^2+...+5^{2002}\right)\)chia hết cho 6
+)A chia hết cho 31
\(A=5+5^2+5^3+...+5^{2004}\)
\(A=\left(5+5^2+5^3\right)+\left(5^4+5^5+5^6\right)+...+\left(5^{2002}+5^{2003}+5^{2004}\right)\)
\(A=\left(5+5^2+5^3\right)+5^3\left(5+5^2+5^3\right)+...+5^{2001}\left(5+5^2+5^3\right)\)
\(A=155+5^3.155+...+5^{2001}.155\)
\(A=155\left(1+5^3+...+5^{2001}\right)\)chia hết cho 31
+) A chia hết cho 156
\(A=5+5^2+5^3+...+5^{2004}\)
\(A=\left(5+5^2+5^3+5^4\right)+\left(5^5+5^6+5^7+5^8\right)+...+\left(5^{2001}+5^{2002}+5^{2003}+5^{2004}\right)\)
\(A=\left(5+5^2+5^3+5^4\right)+5^4\left(5+5^2+5^3+5^4\right)+...+5^{2000}\left(5+5^2+5^3+5^4\right)\)
\(A=780+5^4.780+...+5^{2000}.780\)
\(A=780\left(1+5^4+...+5^{2000}\right)\)chia hết cho 156
b)B=165+2^15 chia hết cho 33
ta có 165 chia hết cho 33
mà 215 ko chia hết cho 33
vậy 165+2^15 không chia hết cho 33 hay B không chia hết cho 33.
19 tháng 8 2019
BN thử vào câu hỏi tương tự xem có k?
Nếu có thì bn xem nhé!
Nếu k thì xin lỗi đã làm phiền bn
Hội con 🐄 chúc bạn học tốt!!!
NT
26 tháng 12 2017
1. \(A=2^{2016}-1\)
\(2\equiv-1\left(mod3\right)\\ \Rightarrow2^{2016}\equiv1\left(mod3\right)\\ \Rightarrow2^{2016}-1\equiv0\left(mod3\right)\\ \Rightarrow A⋮3\)
\(2^{2016}=\left(2^4\right)^{504}=16^{504}\)
16 chia 5 dư 1 nên 16^504 chia 5 dư 1
=> 16^504-1 chia hết cho 5
hay A chia hết cho 5
\(2^{2016}-1=\left(2^3\right)^{672}-1=8^{672}-1⋮7\)
lý luận TT trg hợp A chia hết cho 5
(3;5;7)=1 = > A chia hết cho 105
2;3;4 TT ạ !!