Giải phương trình sau: 3sin2 x – 4 sinx.cosx + 5 cos2 x =2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
26 tháng 8 2019
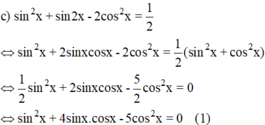
+ Xét cos x = 0 ⇒ sin2x = 1 – cos2x = 1
(1) trở thành 1 = 0 (Vô lý).
+ Xét cos x ≠ 0, chia cả hai vế cho cos2x ta được:
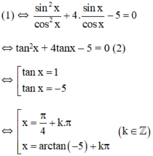
Vậy phương trình có tập nghiệm
(k ∈ Z)
PT
1
CM
31 tháng 7 2017
2sin2x + sinx.cosx – 3cos2x = 0 (1)
+ Xét cos x = 0 ⇒ sin2x = 1 – cos2x = 1
Phương trình (1) trở thành: 2 = 0 (loại)
+ Xét cos x ≠ 0, chia cả hai vế của (1) cho cos2x ta được:
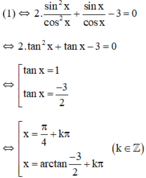
Vậy phương trình có tập nghiệm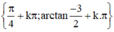 
(k ∈ Z)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
\(\begin{array}{l}a)\;sin2x + cos3x = 0\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) + cos3x = 0\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) = - cos3x\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) = cos\left( {\pi - 3x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{2} - 2x = \pi - 3x + k2\pi \\\frac{\pi }{2} - 2x = - \pi + 3x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + k2\pi \\x = \frac{{3\pi }}{{10}} + k\frac{{2\pi }}{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}b)\;sinx.cosx = \frac{{\sqrt 2 }}{4}\\ \Leftrightarrow \frac{1}{2}\;sin2x = \frac{{\sqrt 2 }}{4}\\ \Leftrightarrow sin2x = \frac{{\sqrt 2 }}{2} = sin\left( {\frac{\pi }{4}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{4} + k2\pi \\2x = \pi - \frac{\pi }{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{8} + k\pi \\x = \frac{{3\pi }}{8} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}c)\;sinx + sin2x = 0\\ \Leftrightarrow sinx = - sin2x\\ \Leftrightarrow sinx = sin( - 2x)\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2x + k2\pi \\x = \pi + 2x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k\frac{{2\pi }}{3}\\x = - \pi + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
DN
1
29 tháng 8 2018
ta có : \(2sin^2x+2cos^4x=2cos^2x+sinx.cosx\)
\(\Leftrightarrow2sin^2x+2cos^2x\left(cos^2x-1\right)-sinx.cosx=0\)
\(\Leftrightarrow2sin^2x-2cos^2x.sin^2x-sinx.cosx=0\)
\(\Leftrightarrow2sin^2x\left(1-cos^2x\right)-sinx.cosx=0\)
\(\Leftrightarrow2sin^4x-sinx.cosx=sinx\left(2sin^3x-cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\2sin^3x-cosx=0\end{matrix}\right.\)
tới đây bn giải như phương trình dạng bình thường nha :)
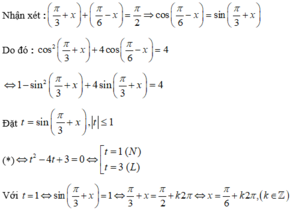
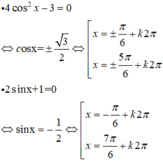
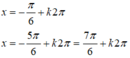
3sin2x – 4sinx.cosx + 5cos2x = 2
⇔ 3sin2x – 4sinx.cosx + 5cos2x = 2(sin2x + cos2x)
⇔ sin2x – 4sinx.cosx + 3 cos2x = 0 (1)
+ Xét cosx = 0 ⇒ sin2x = 1.
Phương trình (1) trở thành 1 = 0 (Vô lý).
+ Xét cos x ≠ 0. Chia hai vế phương trình cho cos2x ta được
Vậy phương trình có tập nghiệm