Biết rằng hai tam giác ABC và A’B’C’ có cùng trọng tâm. Đẳng thức nào sau đây là sai?
A. A A ' → + B B ' ⇀ + C C ' ⇀ = 0 ⇀
B. A A ' → + A B ' → + A C ' → = 0 →
C. A B ' → + B C ' → + C A ' → = 0 →
D. A C ' → + B A ' → + C B ' → = 0 →
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’ nên

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Đáp án D

Đáp án B
A’ = V G ; k ( A ) => − 2 G A ' → = G A → =>Tỉ số vị tự k = – 2

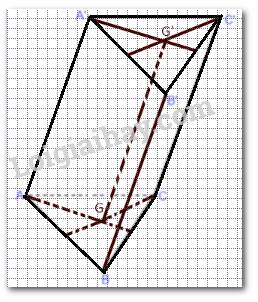
a) Ta có ABC.A'B'C' là hình lăng trụ nên \(\Delta ABC = \Delta A'B'C'\) suy ra AG = A'G'.
Lại có (ABC) // (A'B'C'), giao tuyến của mp(AGG'A') với (ABC) và (A'B'C') lần lượt là AG, A'G' suy ra AG // A'G'.
Như vậy , tứ giác AGG'A' có AG = A'G', AG // A'G' là hình bình hành.
b) AGG'A' là hình bình hành suy ta AA' // GG'.
Lại có AA' // CC' (do ABC.A'B'C' là hình lăng trụ).
Mặt phẳng (AGC) // (A'G'C') suy ra AGC.A'G'C' là hình lăng trụ.
Từ B suy ra A là trọng tâm của tam giác A’B’C’ (vô lí).
Lưu ý các tam giác A’B’C’, B’C’A’, C’A’B’ có cùng trọng tâm.
Đáp án B